题目内容
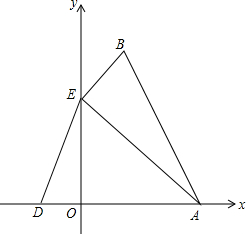 顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.
顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.(1)已知tan∠BAE=
| 1 |
| 3 |
(2)若点P在x轴上,且以O、E、P为顶点的三角形与△ABE相似,求出点P的坐标.
考点:二次函数综合题
专题:
分析:(1)如图1,设抛物线的解析式为y=a(x-3)(x+1),由E(0,3)在抛物线上,代入解析式就可以求出结论,再将解析式化为顶点式就可以求出B的坐标.
(2)根据A、E、B的坐标,由两点间的距离公式及勾股定理的逆定理就可以求出△ABE为直角三角形,如图2,当△AEB∽△POE时,如图3,当△AEB∽△POE时,如图4,当△AEB∽△EOP时,如图5,当△AEB∽△EOP时,由相似三角形的性质分别其求出其值即可.
(2)根据A、E、B的坐标,由两点间的距离公式及勾股定理的逆定理就可以求出△ABE为直角三角形,如图2,当△AEB∽△POE时,如图3,当△AEB∽△POE时,如图4,当△AEB∽△EOP时,如图5,当△AEB∽△EOP时,由相似三角形的性质分别其求出其值即可.
解答:解:(1)如图1,
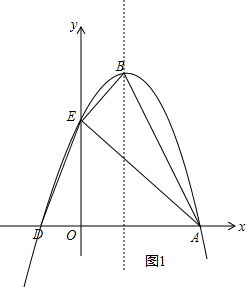
设抛物线的解析式为y=a(x-3)(x+1),由题意,得
3=a(0-3)(0+1),
解得:a=-1,
∴y=-(x-3)(x+1),
∴y=-x2+2x+3
∴y=-(x-1)2+4,
∴抛物线的定点坐标为:(1,4).
∴B(1,4).
答:抛物线的表达式为:y=-x2+2x+3,顶点B的坐标为(1,4);
(2)∵B(1,4),A(3,0),E(0,3),
∴AB2=(1-3)2+(4-0)2=20,AE2=(3-0)2+(0-3)2=18,BE2=(1-0)2+(4-3)2=2,
∴AE2+BE2=18+2=20.
∴AE2+BE2=AB2,
∴△AEB是直角三角形.
∵tan∠BAE=
,
∴
=
.
∵E(0,3),
∴OE=3.
如图2,
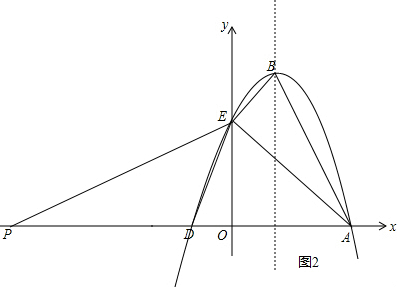
当△AEB∽△POE时
∴
=
,
∴
=
,
∴OP=9,
∴P(-9,0);
如图3,
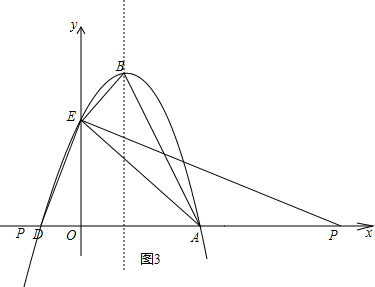
当△AEB∽△POE时,
∴
=
,
∴
=
,
∴OP=9,
∴P(9,0);
如图4,
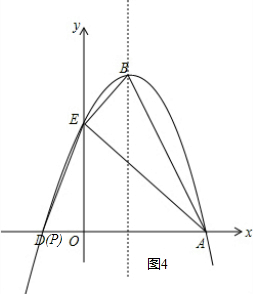
当△AEB∽△EOP时,
∴
=
,
∴
=
,
∴OP=1,
∴P(-1,0);
如图5,
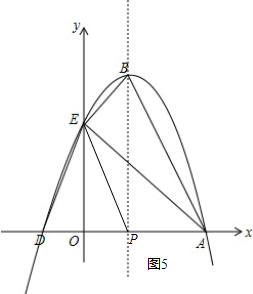
当△AEB∽△EOP时,
∴
=
,
∴
=
,
∴OP=1,
∴P(1,0);
综上所述:P(-9,0),P(9,0),P(-1,0)或P(1,0).

设抛物线的解析式为y=a(x-3)(x+1),由题意,得
3=a(0-3)(0+1),
解得:a=-1,
∴y=-(x-3)(x+1),
∴y=-x2+2x+3
∴y=-(x-1)2+4,
∴抛物线的定点坐标为:(1,4).
∴B(1,4).
答:抛物线的表达式为:y=-x2+2x+3,顶点B的坐标为(1,4);
(2)∵B(1,4),A(3,0),E(0,3),
∴AB2=(1-3)2+(4-0)2=20,AE2=(3-0)2+(0-3)2=18,BE2=(1-0)2+(4-3)2=2,
∴AE2+BE2=18+2=20.
∴AE2+BE2=AB2,
∴△AEB是直角三角形.
∵tan∠BAE=
| 1 |
| 3 |
∴
| BE |
| AE |
| 1 |
| 3 |
∵E(0,3),
∴OE=3.
如图2,

当△AEB∽△POE时
∴
| BE |
| AE |
| OE |
| OP |
∴
| 3 |
| OP |
| 1 |
| 3 |
∴OP=9,
∴P(-9,0);
如图3,

当△AEB∽△POE时,
∴
| BE |
| AE |
| OE |
| OP |
∴
| 3 |
| OP |
| 1 |
| 3 |
∴OP=9,
∴P(9,0);
如图4,

当△AEB∽△EOP时,
∴
| BE |
| AE |
| OP |
| OE |
∴
| 0P |
| 3 |
| 1 |
| 3 |
∴OP=1,
∴P(-1,0);
如图5,

当△AEB∽△EOP时,
∴
| BE |
| AE |
| OP |
| OE |
∴
| 0P |
| 3 |
| 1 |
| 3 |
∴OP=1,
∴P(1,0);
综上所述:P(-9,0),P(9,0),P(-1,0)或P(1,0).
点评:本题考查了待定系数法求二次函数的解析式的运用,抛物线的性质的运用,直角三角形的判定及性质的运用,相似三角形的性质的运用,解答时运用函数的解析式及相似三角形的性质求解是关键.

练习册系列答案
相关题目
一个直角三角形的三条边分别为3、4、5,将这个三角形绕它的直角边所在直线旋转一周得到的几何体的体积是( )
| A、12π |
| B、16π |
| C、12π或16π |
| D、36π或48π |
 如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD.
如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD. 如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为
如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为 已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.
已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°. 如图,AB=AC,OB=OC.求证:∠ADC=∠ADB.
如图,AB=AC,OB=OC.求证:∠ADC=∠ADB.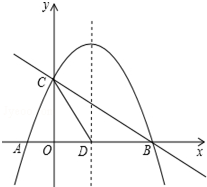 如图,抛物线y=-x2+x+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.
如图,抛物线y=-x2+x+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.