题目内容
 如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为
如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点,连接AE.
(1)AE与BD相等吗?为什么?
(1)当DE=17,AE=15时,求AB的长和S△ADE.
考点:全等三角形的判定与性质
专题:
分析:(1)求出∠ACE=∠BCD,根据SAS推出△ACE≌△BCD即可;
(2)根据全等三角形的性质求出∠B=∠EAC=45°,求出∠EAD=90°,由勾股定理求出AD即可.
(2)根据全等三角形的性质求出∠B=∠EAC=45°,求出∠EAD=90°,由勾股定理求出AD即可.
解答:解:(1)AE=BD,
理由是:∵∠ACD=∠DCE=90°,
∴∠ACE=∠BCD=90°-∠ACD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)∵△ACE≌△BCD,
∴∠B=∠EAC=45°,
∴∠EAD=45°+45°=90°,
∴△EAD是直角三角形,
由勾股定理得:AD=
=
=8,
∵BD=AE=15,
∴AB=AD+BD=8+15=23.
理由是:∵∠ACD=∠DCE=90°,
∴∠ACE=∠BCD=90°-∠ACD,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)∵△ACE≌△BCD,
∴∠B=∠EAC=45°,
∴∠EAD=45°+45°=90°,
∴△EAD是直角三角形,
由勾股定理得:AD=
| DE2-AE2 |
| 172-152 |
∵BD=AE=15,
∴AB=AD+BD=8+15=23.
点评:本题考查了全等三角形的性质和判定,勾股定理的应用,解此题的关键是推出△ACE≌△BCD,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
若(a-1)2+|b+2|=0,则(a+b)2014的值是( )
| A、-1 | B、1 | C、0 | D、2014 |
下列计算正确的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
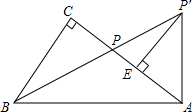 如图,在Rt△ABC中,∠C=90°,AP′⊥AB,BP′交AC于点P,AP=AP′.
如图,在Rt△ABC中,∠C=90°,AP′⊥AB,BP′交AC于点P,AP=AP′.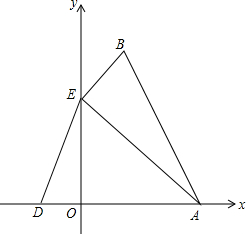 顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.
顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.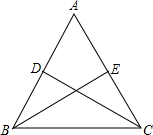 已知:△ABC中,AB=AC,D、E分别为AB、AC的中点,求证:∠ABE=∠ACD.
已知:△ABC中,AB=AC,D、E分别为AB、AC的中点,求证:∠ABE=∠ACD. 如图,已知:∠E=∠F,∠B=∠C,AE=AF,试说明:(1)△ABE≌△ACF;(2)BM=CN.
如图,已知:∠E=∠F,∠B=∠C,AE=AF,试说明:(1)△ABE≌△ACF;(2)BM=CN.