题目内容
 如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD.
如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD.考点:全等三角形的判定与性质
专题:证明题
分析:过D分别作直线BC、AC垂线,分别交于F、G点,则DE=DG,可证△DEF≌△DAG,即可解题.
解答:解:过D分别作直线BC、AC垂线,分别交于F、G点,则DE=DG,

∵AB=AC,∠A=100°
∴∠B=∠ACB=40°,
∵BE=DE∴∠B=∠BDE=40°,
∵CD平分∠ACB
∴∠ACD=∠BCD=20°
∴∠CDE=∠CDB-∠BDE=180°-∠B-∠BCD-∠BDE=80°,
∴∠CED=180°-80°-20°=80°,
∴CD=CE,
∵DF⊥BC,DG⊥CG,
∴∠DAG=180°-∠DAC=80°,
∵在△DEF和△DAG中,
,
∴△DEF≌△DAG(AAS),
∴DE=DA=BE,
∴BC=CE+BE=CD+AD.

∵AB=AC,∠A=100°
∴∠B=∠ACB=40°,
∵BE=DE∴∠B=∠BDE=40°,
∵CD平分∠ACB
∴∠ACD=∠BCD=20°
∴∠CDE=∠CDB-∠BDE=180°-∠B-∠BCD-∠BDE=80°,
∴∠CED=180°-80°-20°=80°,
∴CD=CE,
∵DF⊥BC,DG⊥CG,
∴∠DAG=180°-∠DAC=80°,
∵在△DEF和△DAG中,
|
∴△DEF≌△DAG(AAS),
∴DE=DA=BE,
∴BC=CE+BE=CD+AD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证AD=BE是解题的关键.

练习册系列答案
相关题目
方程y2-y+
=0的两根的情况是( )
| 1 |
| 4 |
| A、没有实数根 |
| B、有两个不相等的实数根 |
| C、有两个相等的实数根 |
| D、不能确定 |
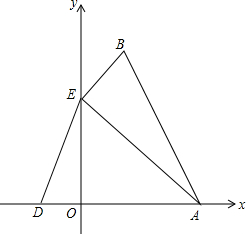 顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.
顶点在B点的抛物线y=ax2+bx+c交x轴于点A(3,0),D(-1,0),交y轴于点E(0,3),连接AB、AE、BE.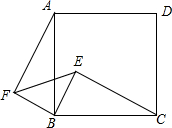 已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连结AF.
已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连结AF. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=36°,则∠3=
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=24°,∠2=36°,则∠3=