题目内容
（1）如图1，D、E分别是等边△ABC两边AC、BC上的点，且AD=CE，BD与AE交于F，求∠AFD的度数．
（2）如图2，若D、E分别是等边△ABC两边AC、CB延长线上的点，且AD=CE，BD与AE交于F，求∠AFD的度数．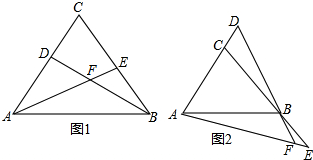
（2）如图2，若D、E分别是等边△ABC两边AC、CB延长线上的点，且AD=CE，BD与AE交于F，求∠AFD的度数．
考点：全等三角形的判定与性质,等边三角形的性质
专题：计算题
分析：（1）可证△ADB≌△CEA，得∠CAE=∠DBA，即可求得∠AFD的值；
（2）可证△ADB≌△CEA，得∠D=∠E，即可求得∠AFD=∠ACB．
（2）可证△ADB≌△CEA，得∠D=∠E，即可求得∠AFD=∠ACB．
解答：解：（1）在△ADB和△CEA中，
，
∴△ADB≌△CEA（SAS），
∴∠ABD=∠CAE，
∴∠AFD=∠DBA+∠BAE=∠BAE+∠CAE=60°．
（2））在△ADB和△CEA中，
，
∴△ADB≌△CEA（SAS），
∴∠D=∠E，
∴∠AFD=∠E+∠EBF=∠D+∠CBD=∠ACB=60°．
|
∴△ADB≌△CEA（SAS），
∴∠ABD=∠CAE，
∴∠AFD=∠DBA+∠BAE=∠BAE+∠CAE=60°．
（2））在△ADB和△CEA中，
|
∴△ADB≌△CEA（SAS），
∴∠D=∠E，
∴∠AFD=∠E+∠EBF=∠D+∠CBD=∠ACB=60°．
点评：本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证△ADB≌△CEA是解题的关键．
练习册系列答案
相关题目
若4a2+18ab+m是一个完全平方式，则m等于（ ）
| A、9b2 | ||
| B、18b2 | ||
| C、81b2 | ||
D、
|
在下列各数
，2
，
，
，-
，
，0.
，
，
，0.101001000100001中，无理数有（ ）
| 144 |
| 2 |
| 3 | 9 |
| 3 | -1 |
| 1 |
| 7 |
| 3 | 16 |
| • |
| 3 |
| π |
| 2 |
| 25 |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，等腰△ABC中，AC=BC，△BDC和△ACE分别为等边三角形，AE与BD相交于点F，连接CF并延长，交AB于点G．求证：G为AB的中点．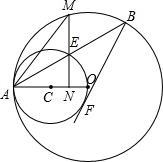
如图，OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AB交于点E．
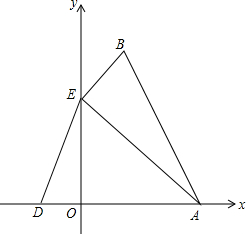顶点在B点的抛物线y=ax2+bx+c交x轴于点A（3，0），D（-1，0），交y轴于点E（0，3），连接AB、AE、BE．