题目内容
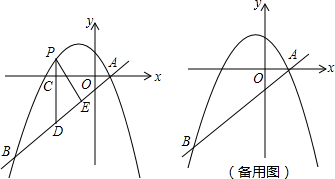
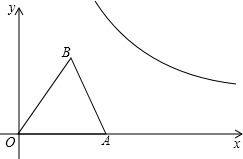 如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).
如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数y=
| 32 |
| x |
考点:待定系数法求一次函数解析式,反比例函数图象上点的坐标特征,等腰三角形的性质,平移的性质
专题:
分析:(1)过点B作BC⊥x轴于点C.由勾股定理可得 OB=5.再由OA=OB,得点A的坐标为(5,0),设直线AB的解析式为 y=kx+b,代入A、B两点坐标可求直线AB的解析式为y=-2x+10.
(2)将等腰△AOB沿x轴正方向平移5个单位,能使点B落在反比例函数y=
(x>0)的图象上.
(2)将等腰△AOB沿x轴正方向平移5个单位,能使点B落在反比例函数y=
| 32 |
| x |
解答: 解:(1)过点B作BC⊥x轴于点C,
解:(1)过点B作BC⊥x轴于点C,
∵点B的坐标为(3,4),
∴由勾股定理可得 OB=5,
∵OA=OB,
∴点A的坐标为(5,0);
设直线AB的解析式为 y=kx+b,
把A、B两点坐标可求直线AB的解析式,得
,
解得
,
∴直线AB的解析式为y=-2x+10;
(2)设将等腰△AOB沿x轴正方向平移a个单位,能使点B落在反比例函数y=
(x>0)的图象上.
∵点B的坐标为(3,4),
∴平移后点B坐标为(3+a,4),
∴4(3+a)=32,
解得a=5,
∴将等腰△AOB沿x轴正方向平移5个单位,能使点B落在反比例函数y=
(x>0)的图象上.
 解:(1)过点B作BC⊥x轴于点C,
解:(1)过点B作BC⊥x轴于点C,∵点B的坐标为(3,4),
∴由勾股定理可得 OB=5,
∵OA=OB,
∴点A的坐标为(5,0);
设直线AB的解析式为 y=kx+b,
把A、B两点坐标可求直线AB的解析式,得
|
解得
|
∴直线AB的解析式为y=-2x+10;
(2)设将等腰△AOB沿x轴正方向平移a个单位,能使点B落在反比例函数y=
| 32 |
| x |
∵点B的坐标为(3,4),
∴平移后点B坐标为(3+a,4),
∴4(3+a)=32,
解得a=5,
∴将等腰△AOB沿x轴正方向平移5个单位,能使点B落在反比例函数y=
| 32 |
| x |
点评:本题考查了待定系数法求一次函数的解析式、反比例函数图象上点的坐标特征、等腰三角形的性质以及平移的性质和规律,向右平移时,横坐标加上平移的单位长度,向左平移时横坐标减去平移的单位长度.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
两圆的半径分别为3和7,圆心距为6,则两圆的交点个数为( )
| A、1个 | B、2个 |
| C、0个 | D、以上都不对 |
在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
| A、50° | B、45° |
| C、40° | D、30° |
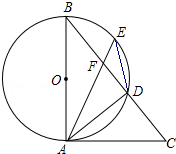 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是
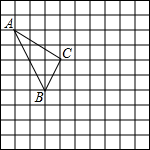 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).