题目内容
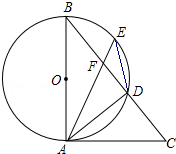 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是 |
| BD |
(1)求证:AC是⊙O的切线;
(2)若点E是
 |
| BD |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)欲证明AC是⊙O的切线,只需证得AB⊥AC即可;
(2)通过相似三角形(△ADC∽△BAC)的对应边成比例求得AC=6.由圆周角、弧、弦间的关键推知CA=CF=6,故DF=CA-CD=2.
(2)通过相似三角形(△ADC∽△BAC)的对应边成比例求得AC=6.由圆周角、弧、弦间的关键推知CA=CF=6,故DF=CA-CD=2.
解答:解:(1)∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°.
∵∠B=∠AED=∠CAD,∠C=∠C,∴∠C+∠CAD=∠C+∠B=90°.
∴∠BAC=∠ADC=90°.
即AB⊥AC于点A.
又∵AB是⊙O的直径,
∴AC是⊙O的切线;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠BAC=∠ADB=90°,
∴∠ACD=∠BCA,
∴△ADC∽△BAC.
∴
=
.即AC2=BC×CD=36.
解得 AC=6.
∵点E是
的中点,
∴∠DAE=∠BAE.
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2.
∴∠ADB=∠ADC=90°.
∵∠B=∠AED=∠CAD,∠C=∠C,∴∠C+∠CAD=∠C+∠B=90°.
∴∠BAC=∠ADC=90°.
即AB⊥AC于点A.
又∵AB是⊙O的直径,
∴AC是⊙O的切线;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠BAC=∠ADB=90°,
∴∠ACD=∠BCA,
∴△ADC∽△BAC.
∴
| AC |
| BC |
| CD |
| AC |
解得 AC=6.
∵点E是
 |
| BD |
∴∠DAE=∠BAE.
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2.
点评:本题考查了切线的判定、相似三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2014年3月5日,第十二届全国人民代表大会第二次会议在人民大会堂开幕,国务院总理李克强作《政府工作报告》.报告指出我国2013年国内生产总值达到569000亿元.“569000”这个数据用科学记数法(保留两个有效数字)表示正确的是( )
| A、5.69×105 |
| B、5.69×106 |
| C、5.7×105 |
| D、6.0×106 |
 如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.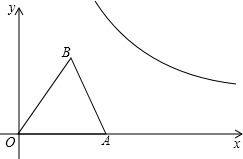 如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).
如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).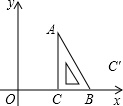 如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一限象内,∠ACB=90°,∠CAB=30°,AC=4
如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一限象内,∠ACB=90°,∠CAB=30°,AC=4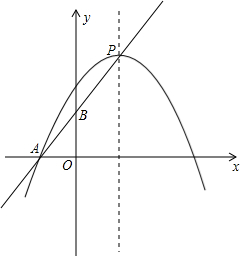 已知直线y=kx+3-k,当k=1,k=
已知直线y=kx+3-k,当k=1,k= 已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.
已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC. 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.