题目内容
某种植基地计划种植A、B两种水果共30亩,已知这两种水果的年产量分别为300千克/亩、320千克/亩,收购单价分别是6元/千克、7元/千克.
(1)若该基地收获两种水果的年总产量为9320千克,求两种水果各种植了多少亩?
(2)设该基地种植A种水果a亩,全部收购该基地水果的年总收入为w元,求出w与a的函数关系式.若要求种植A种水果的亩数不少于B种的一半,那么种植A、B两种水果各多少亩时,全部收购该基地水果的年总收入最多?最多是多少元?
(1)若该基地收获两种水果的年总产量为9320千克,求两种水果各种植了多少亩?
(2)设该基地种植A种水果a亩,全部收购该基地水果的年总收入为w元,求出w与a的函数关系式.若要求种植A种水果的亩数不少于B种的一半,那么种植A、B两种水果各多少亩时,全部收购该基地水果的年总收入最多?最多是多少元?
考点:一次函数的应用
专题:
分析:(1)根据总产量的等量关系,可得一元一次方程,根据解一元一次方程,可得答案;
(2)根据种植面积的关系,可得a的取值范围,根据一次函数的性质,可得答案.
(2)根据种植面积的关系,可得a的取值范围,根据一次函数的性质,可得答案.
解答:解:(1)设该基地种植A种水果x亩,种植B种水果(30-x)亩,根据题意得
300x+320(30-x)=9320
解得x=14,
∴30-x=16
答:种植A种水果14亩,种植B种水果16亩;
(2)设该基地种植A种水果a亩,种植B种水果(30-a)亩,由题意得:
a≥
(30-a),
解得 a≥10.
根据题意得:w=6×300a+7×320(30-a)=-440a+67200
即w=-440a+67200
∵w随a的增大而减小
∴.当a最小=10时,30-a=20,
w最大=-440×10+67200=62800
答:种植A种水果10亩,种植B种水果20亩时,全部收购该基地水果的年总收入最多为62800元.
300x+320(30-x)=9320
解得x=14,
∴30-x=16
答:种植A种水果14亩,种植B种水果16亩;
(2)设该基地种植A种水果a亩,种植B种水果(30-a)亩,由题意得:
a≥
| 1 |
| 2 |
解得 a≥10.
根据题意得:w=6×300a+7×320(30-a)=-440a+67200
即w=-440a+67200
∵w随a的增大而减小
∴.当a最小=10时,30-a=20,
w最大=-440×10+67200=62800
答:种植A种水果10亩,种植B种水果20亩时,全部收购该基地水果的年总收入最多为62800元.
点评:本题考查了一次函数的应用,(1)找等量关系列方程是解题关键;(2)先求出a的取值范围,再利用一次函数的性质,得出答案.

练习册系列答案
相关题目
据《都市快报》,2014年杭州市将投入1.3亿元,用来搞好学校食堂维修改造、改善食堂硬件,全面实施食品卫生监督量化分级管理制度.其中1.3亿精确到( )
| A、个分位 | B、十分位 |
| C、百万位 | D、千万位 |
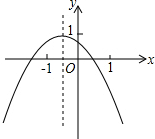 如图所示的二次函数图象,以下四个结论:
如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.
你认为正确的有( )
| A、2个 | B、4个 | C、3个 | D、1个 |
 如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
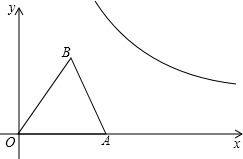 如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).
如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4). 已知直线y=kx+3-k,当k=1,k=
已知直线y=kx+3-k,当k=1,k=