题目内容
18.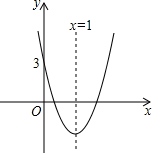 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:①b2-4ac<0,②abc<0,③4a+2b+c=1,④a-b+c>0中,判断正确的有( )
| A. | ②③④ | B. | ①②③ | C. | ②③ | D. | ①④ |
分析 根据平移后的图象即可判定①,根据平移后的对称轴和与y轴的交点坐标,即可判定a和b的关系以及c的值,即可判定②,根据与y轴的交点求得对称点,即可判定③,根据图象即可判定④.
解答 解:根据题意平移后的抛物线的对称轴x=-$\frac{b}{2a}$=1,c=3-2=1,
由图象可知,平移后的抛物线与x轴有两个交点,
∴b2-4ac>0,故①错误;
∵抛物线开口向上,∴a>0,b=-2a<0,
∴abc<0,故②正确;
∵平移后抛物线与y轴的交点为(0,1)对称轴x=1,
∴点(2,1)点(0,1)的对称点,
∴当x=2时,y=1,
∴4a+2b+c=1,故③正确;
由图象可知,当x=-1时,y>0,
∴a-b+c>0,故④正确.
故选A.
点评 本题考查二次函数的图象与几何变换,二次函数图象与系数之间的关系,解题的关键是可以看懂二次函数的图象,根据图象可以判断a、b、c的符号,灵活变化,能够找出所求各结论需要的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.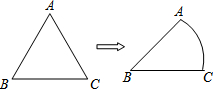 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )| A. | ($\frac{60}{π}$)° | B. | ($\frac{90}{π}$)° | C. | ($\frac{120}{π}$)° | D. | ($\frac{180}{π}$)° |
7.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |