题目内容
4.在直角坐标系中,直线l是经过点(2,0)且平行于y轴的直线,若点P(a,-2)与点Q(4,b)关于直线l成对称,则a-b=-2.分析 首先根据直线l的性质写出直线l的解析式,根据P、Q两点关于直线l对称,得出PQ中点在直线l上,求出PQ中点坐标,代入直线l即可求出a、b值,进而得出答案.
解答 解:∵直线l是经过点(2,0)且平行于y轴的直线,
∴直线l的解析式为:x=2,
∵点P(a,-2)与点Q(4,b)关于直线l成对称,
∴PQ的中点在直线l上,
利用中点坐标公式得PQ中点坐标:($\frac{a+4}{2}$,$\frac{b-2}{2}$),
将点($\frac{a+4}{2}$,$\frac{b-2}{2}$)代入直线l得:
$\frac{a+4}{2}$=2,$\frac{b-2}{2}$=0,
解得:a=0,b=2,
∴a-b=0-2=-2.
故答案为:-2.
点评 题目考查了坐标与图形的对称变化,实质上是考察中点坐标公式,学生应该牢记中点坐标公式($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),此类问题就会迎刃而解.

练习册系列答案
相关题目
15.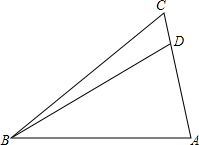 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.
 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.
19.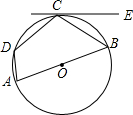 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )| A. | 145° | B. | 125° | C. | 90° | D. | 80° |
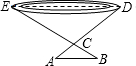 如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.
如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE. 如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,
如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,