题目内容
11. 如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.
如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.
分析 延长AD至A′,使AD=DA′,延长AB至E′,使BE=BE′,连接A′E′,交BC于M,交DC于N,此时AN=A′N,EM=E′M,四边形AEMN周长=AN+MN+ME+AE=A′B′+AE,根据两点之间线段最短,A′B′+AE就是四边形AEMN周长的最小值;然后根据勾股定理即可求得.
解答  解:延长AD至A′,使AD=DA′,延长AB至E′,使BE=BE′,连接A′E′,交BC于M,交DC于N,此时AN=A′N,EM=E′M,四边形AEMN周长=AN+MN+ME+AE=A′E′+AE,根据两点之间线段最短,A′E′+AE就是四边形AEMN周长的最小值;
解:延长AD至A′,使AD=DA′,延长AB至E′,使BE=BE′,连接A′E′,交BC于M,交DC于N,此时AN=A′N,EM=E′M,四边形AEMN周长=AN+MN+ME+AE=A′E′+AE,根据两点之间线段最短,A′E′+AE就是四边形AEMN周长的最小值;
∵AD=2,AE=BE=1,
∴A′D=AD=2,BE=BE′=1,
∴AE′=3,AA′=4,
∴A′E′=$\sqrt{AE{′}^{2}+AA{′}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴四边形AEMN周长的最小值为5+1=6.
故答案为6.
点评 本题考查了轴对称-最短路线问题,同时也考查了正方形的性质,轴对称的性质,勾股定理的应用等,作出M、N的点是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.
如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N. 如图,矩形OABC中,O是数轴的原点,OC在数轴上,OC=3,OA=1,若以点O为圆心,对角线OB长为半径作弧交数轴的正半轴于M,则点M表示的数为$\sqrt{10}$.
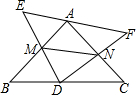
如图,矩形OABC中,O是数轴的原点,OC在数轴上,OC=3,OA=1,若以点O为圆心,对角线OB长为半径作弧交数轴的正半轴于M,则点M表示的数为$\sqrt{10}$. 如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.
如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.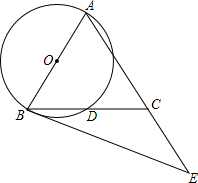 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.