题目内容
6. 如图,矩形OABC中,O是数轴的原点,OC在数轴上,OC=3,OA=1,若以点O为圆心,对角线OB长为半径作弧交数轴的正半轴于M,则点M表示的数为$\sqrt{10}$.
如图,矩形OABC中,O是数轴的原点,OC在数轴上,OC=3,OA=1,若以点O为圆心,对角线OB长为半径作弧交数轴的正半轴于M,则点M表示的数为$\sqrt{10}$.
分析 首先根据勾股定理计算出OB的长,进而得到OM的长,再根据O点为原点,可得M点表示的数.
解答 解:∵四边形OABC为矩形,OA=1,∴BC=1,
又OC=3,∠C=90°,
由勾股定理得,OB=$\sqrt{10}$,
∴OM=$\sqrt{10}$,
则点M表示的数为:$\sqrt{10}$.
点评 本题考查的是实数与数轴的关系和勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边边长的平方.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
14.下列调查中,适合用普查方式的是( )
| A. | 了解瘦西湖风景区中鸟的种类 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解学生对“扬农”牌牛奶的喜爱情况 | |
| D. | 航天飞机发射前的安全检查 |
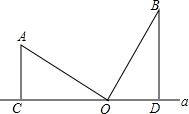 如图,在直线a有上一点O,线段OA绕点O顺时旋转90°到线段OB位置,作BD⊥a,AC⊥a,求证:CD=AC+BD.
如图,在直线a有上一点O,线段OA绕点O顺时旋转90°到线段OB位置,作BD⊥a,AC⊥a,求证:CD=AC+BD. 如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.
如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.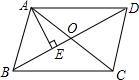 如图,已知?ABCD的对角线AC与BC相交于点O,AE⊥BD于点E,∠DAE=60°,AE=2cm,AC+BD=12cm,求△BOC的周长.
如图,已知?ABCD的对角线AC与BC相交于点O,AE⊥BD于点E,∠DAE=60°,AE=2cm,AC+BD=12cm,求△BOC的周长. 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.