题目内容
1．先化简，再求值：$\frac{y-3}{y-2}÷（y+2-\frac{5}{y-2}）-\frac{1}{y}$，其中y是方程y2+3y-4=0的解．分析 先根据分式混合运算的法则把原式进行化简
解答 解：原式=$\frac{y-3}{y-2}$•$\frac{y-2}{（y+3）（y-3）}$-$\frac{1}{y}$
=$\frac{1}{y+3}$-$\frac{1}{y}$
=$\frac{-3}{{y}^{2}+3y}$，
∵y是方程y2+3y-4=0的解，
∴y2=4-3y，
∴原式=$\frac{-3}{4-3y+3y}$=-$\frac{3}{4}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
如图所示，E为边长是2的正方形ABCD的中点，M为BC上一点，N为CD上一点，连EM、MN、NA，则四边形AEMN周长的最小值为6．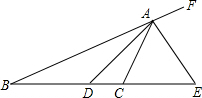
如图，AD是△ABC中∠BAC的平分线，AE是△ABC的外角平分线，AE交BC的延长线于点E，∠BAD=20°，∠E=50°，求∠ACD的度数．