题目内容
2.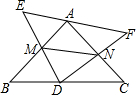 如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.
如图,△ABC和△DEF均为等腰直角三角形,∠A=∠D=90°,D为BC的中点,当△DEF绕D旋转,使DE、DF分别交边AB、AC于M、N.(1)求证:DM=DN;
(2)当BC=2$\sqrt{2}$时,求四边形AMDN的面积;
(3)若△ABC的面积为S,△MAN的面积有最大值还是有最小值?并求出这个最值.
分析 (1)根据等腰直角三角形性质得出AD=DC,AD⊥BC,∠C=∠MAD=45°,求出∠ADM=∠CDN,根据全等三角形的判定推出即可;
(2)求出四边形AMDN的面积等于三角形ADC的面积,即可求出答案;
(3)求出AM+AN=AC,根据面积求出AC长,根据三角形的面积得出二次函数解析式,求出最值即可.
解答 (1)证明:连接AD,
∵△BAC是等腰直角三角形,D为斜边BC中点,
∴AD=DC,AD⊥BC,∠C=∠MAD=45°,
∵∠EDF=∠ADC=90°,
∴∠ADM=∠CDN=90°-∠ADF,
在△ADM和△CDN中,
$\left\{\begin{array}{l}{∠MAD=∠C}\\{AD=DC}\\{∠ADM=∠CDN}\end{array}\right.$,
∴△ADM≌△CDN(ASA),
∴DM=DN;
(2)解:∵△BAC是等腰直角三角形,D为斜边BC中点,BC=2$\sqrt{2}$,
∴AD⊥BC,AD=DB=BD=$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2,
∵△ADM≌△CDN,
∴S△ADM=S△CDN,
∴S四边形AMDN=S△ADM+S△ADN
=S△CDN+S△ADN
=S△ADC
=$\frac{1}{2}$S△ABC
=$\frac{1}{2}$×2
=1;
(3)解:设AC=AB=x,
∵△ABC的面积为S,
∴$\frac{1}{2}$x2=S,
∴x=$\sqrt{2S}$,
即AC=AB=$\sqrt{2S}$,
∵△ADM≌△CDN,
∴AM=CN,
∴AM+AN=AC=$\sqrt{2S}$,
S△MAN=$\frac{1}{2}$AM×AN
=$\frac{1}{2}$AM($\sqrt{2S}$-AM)
=-$\frac{1}{2}$AM2+$\frac{\sqrt{2S}}{2}$AM,
∵-$\frac{1}{2}$<0,
∴开口向下,有最大值,
最大值为:$\frac{4×(-\frac{1}{2})×0-(\frac{\sqrt{2S}}{2})^{2}}{4×(-\frac{1}{2})}$=$\frac{S}{4}$.
点评 本题考查了等腰直角三角形性质,全等三角形的判定和性质,二次函数的最值的应用,能求出二次函数的解析式和求出△ADM≌△CDN是解此题的关键,难度偏大.


| A. | 12π | B. | 2π | C. | π | D. | 3π |
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | 了解瘦西湖风景区中鸟的种类 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解学生对“扬农”牌牛奶的喜爱情况 | |
| D. | 航天飞机发射前的安全检查 |
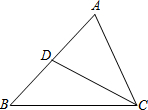 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求: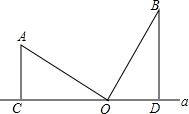 如图,在直线a有上一点O,线段OA绕点O顺时旋转90°到线段OB位置,作BD⊥a,AC⊥a,求证:CD=AC+BD.
如图,在直线a有上一点O,线段OA绕点O顺时旋转90°到线段OB位置,作BD⊥a,AC⊥a,求证:CD=AC+BD. 如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.
如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.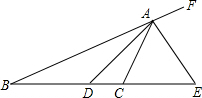 如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.