题目内容
3. 如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.
如图所示.在?ABCD中分别以BC、AB为边画等边三角形BCF、ABE,连接DE、DF.求证:△DEF是等边三角形.
分析 等边三角形中,三条边相等,三个角都是60°,则由60°角及平行四边形对角相等的性质可得∠DAE=∠DCF,即△DAE≌△FCD,得出DF=DE,同理可得出三条边都相等,进而可得出结论.
解答 证明:∵△ABE和△BCF都是等边三角形,
∴AE=AB=CD,CF=BC=AD,
∴∠BAE=∠BCF=60°,即∠DAE+∠BAD=∠DCF+∠BCD,
在平行四边形ABCD中,则∠BAD=∠BCD,
∴∠DAE=∠DCF,
在△DAE与△FCD中,
$\left\{\begin{array}{l}{AD=CF}\\{∠DAE=∠FCD}\\{AE=CD}\end{array}\right.$,
∴△DAE≌△FCD(SAS),
∴DF=DE,∠EAD=∠DCF,
设∠ABC=β,则∠BAD=180°-β,
∴∠EBF=360°-2×60°-β=240°-β,∠EAD=60°+(180°-β)=240°-β,
∴∠EBF=∠EAD
∵EA=EB,AD=BC=BF,
在△BEF与△AED中,
$\left\{\begin{array}{l}{AE=BE}\\{∠EAD=∠EBF}\\{AD=BF}\end{array}\right.$,
∴△BEF≌△AED(SAS),
∴DE=EF,
∴DE=DF=EF,
即△DEF是等边三角形.
点评 本题主要考查了平行四边形的性质及全等三角形的判定及性质,能够熟练掌握,并能够进行一些简单的证明、计算问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
13.某几何体的主视图、左视图和俯视图分別如图,则该几何体的体积为( )


| A. | 12π | B. | 2π | C. | π | D. | 3π |
14.下列调查中,适合用普查方式的是( )
| A. | 了解瘦西湖风景区中鸟的种类 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解学生对“扬农”牌牛奶的喜爱情况 | |
| D. | 航天飞机发射前的安全检查 |
 如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.
如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为6.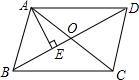 如图,已知?ABCD的对角线AC与BC相交于点O,AE⊥BD于点E,∠DAE=60°,AE=2cm,AC+BD=12cm,求△BOC的周长.
如图,已知?ABCD的对角线AC与BC相交于点O,AE⊥BD于点E,∠DAE=60°,AE=2cm,AC+BD=12cm,求△BOC的周长.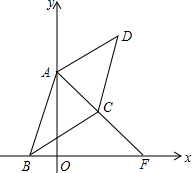 如图,若A(0,a),B(b,0),C(c,c),且(a-5)2+|b+2|+$\sqrt{c-3}$=0.四边形ABCD为平行四边形,点D在第一象限,直线AC交x轴于点F.
如图,若A(0,a),B(b,0),C(c,c),且(a-5)2+|b+2|+$\sqrt{c-3}$=0.四边形ABCD为平行四边形,点D在第一象限,直线AC交x轴于点F. 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=AB=1cm,CD=$\sqrt{3}$cm,求梯形ABCD的面积.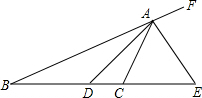 如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.
如图,AD是△ABC中∠BAC的平分线,AE是△ABC的外角平分线,AE交BC的延长线于点E,∠BAD=20°,∠E=50°,求∠ACD的度数.