题目内容
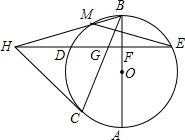如图，AB，BC分别是⊙O的直径和弦，点D为 |
| BC |
（1）求证：点B为弧DE的中点；
（2）求证：∠HMD=∠MHE+∠MEH；
（3）若HC=3BG，⊙O的半径为4，tan∠ABC=
| 3 |
| 4 |
考点：圆的综合题,三角形的外角性质,等腰三角形的性质,勾股定理,相似三角形的判定与性质
专题：综合题
分析：（1）连接OC，如图1，根据切线的性质可得∠OCH=90°，要证点B为弧DE的中点，根据垂径定理只需证明∠BFG=∠OCH=90°即可；
（2）连接BE，如图2，要证∠HMD=∠MHE+∠MEH，只需证∠HMD=∠BME，根据圆内接四边形的性质可得∠HMD=∠BED，只需证到∠BED=∠BME即可；
（3）作HN⊥BC于点N，连接AC、OD，如图3．在Rt△BFG中，设FG=3k，则有FB=4k，BG=5k，HG=HC=3BG=15k．易证△HNG∽△BFG，根据相似三角形的性质可求得GN=9k．由HG=HC，HN⊥GC可得CN=GN=9k，从而可得BC=23k，进而得到AB=
BC=
k，根据⊙O的半径为4可求出k，从而可求出FG、BF、HC、OF，在Rt△DFO中，运用勾股定理可求出DF，就可求出DG的值．
（2）连接BE，如图2，要证∠HMD=∠MHE+∠MEH，只需证∠HMD=∠BME，根据圆内接四边形的性质可得∠HMD=∠BED，只需证到∠BED=∠BME即可；
（3）作HN⊥BC于点N，连接AC、OD，如图3．在Rt△BFG中，设FG=3k，则有FB=4k，BG=5k，HG=HC=3BG=15k．易证△HNG∽△BFG，根据相似三角形的性质可求得GN=9k．由HG=HC，HN⊥GC可得CN=GN=9k，从而可得BC=23k，进而得到AB=
| 5 |
| 4 |
| 115 |
| 4 |
解答：证明：（1）连接OC，如图1，
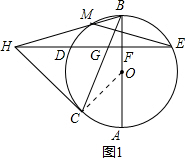
∵HC=HG，
∴∠HCG=∠HGC；
∵HC切⊙O于C点，
∴∠OCB+∠HCG=90°；
∵OB=OC，
∴∠OCB=∠OBC，
∵∠HGC=∠BGF，
∴∠OBC+∠BGF=90°，
∴∠BFG=90°，即DE⊥AB；
∵AB是直径，
∴点B为弧DE的中点；
（2）连接BE，
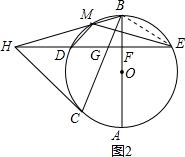
由（1）知
=
，
∴∠BED=∠BME；
∵四边形BMDE内接于⊙O，
∴∠HMD=∠BED，
∴∠HMD=∠BME；
∵∠BME是△HEM的外角，
∴∠BME=∠MHE+∠MEH，
∴∠HMD=∠MHE+∠MEH；
（3）作HN⊥BC于点N，连接AC、OD，如图3．
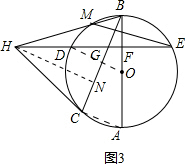
则有∠HNG=90°．
在Rt△BFG中，
tan∠FBG=
=
．
设FG=3k，则FB=4k，
∴BG=
=5k，
∴HG=HC=3BG=15k．
∵∠HNG=∠BFG=90°，∠HGN=∠BGF，
∴△HNG∽△BFG，
∴
=
，
∴
=
，
∴GN=9k．
∵HG=HC，HN⊥GC，
∴CN=GN=9k，
∴BC=BG+GN+NC=5k+9k+9k=23k．
∵AB是⊙O的直径，
∴∠ACB=90°，
∴tan∠ABC=
=
，
∴AC=
BC，
∴AB=
=
BC=
k．
∵⊙O的半径为4，
∴
k=8，
∴k=
，
∴FG=3k=
，BF=4k=
，HC=15k=
，
∴OF=OB-BF=4-
=
．
在Rt△DFO中，
DF=
=
=
，
∴DG=DF-GF=
-
=
．
∴HC的长度为
，DG的长度为
．
∵HC=HG，
∴∠HCG=∠HGC；
∵HC切⊙O于C点，
∴∠OCB+∠HCG=90°；
∵OB=OC，
∴∠OCB=∠OBC，
∵∠HGC=∠BGF，
∴∠OBC+∠BGF=90°，
∴∠BFG=90°，即DE⊥AB；
∵AB是直径，
∴点B为弧DE的中点；
（2）连接BE，
由（1）知
|
| BD |
|
| BE |
∴∠BED=∠BME；
∵四边形BMDE内接于⊙O，
∴∠HMD=∠BED，
∴∠HMD=∠BME；
∵∠BME是△HEM的外角，
∴∠BME=∠MHE+∠MEH，
∴∠HMD=∠MHE+∠MEH；
（3）作HN⊥BC于点N，连接AC、OD，如图3．
则有∠HNG=90°．
在Rt△BFG中，
tan∠FBG=
| FG |
| FB |
| 3 |
| 4 |
设FG=3k，则FB=4k，
∴BG=
| FG2+BF2 |
∴HG=HC=3BG=15k．
∵∠HNG=∠BFG=90°，∠HGN=∠BGF，
∴△HNG∽△BFG，
∴
| GN |
| GF |
| GH |
| BG |
∴
| GN |
| 3k |
| 15k |
| 5k |
∴GN=9k．
∵HG=HC，HN⊥GC，
∴CN=GN=9k，
∴BC=BG+GN+NC=5k+9k+9k=23k．
∵AB是⊙O的直径，
∴∠ACB=90°，
∴tan∠ABC=
| AC |
| BC |
| 3 |
| 4 |
∴AC=
| 3 |
| 4 |
∴AB=
| AC2+BC2 |
| 5 |
| 4 |
| 115 |
| 4 |
∵⊙O的半径为4，
∴
| 115 |
| 4 |
∴k=
| 32 |
| 115 |
∴FG=3k=
| 96 |
| 115 |
| 128 |
| 115 |
| 96 |
| 23 |
∴OF=OB-BF=4-
| 128 |
| 115 |
| 332 |
| 115 |
在Rt△DFO中，
DF=
| OD2-OF2 |
42-(
|
96
| ||
| 115 |
∴DG=DF-GF=
96
| ||
| 115 |
| 96 |
| 115 |
96
| ||
| 115 |
∴HC的长度为
| 96 |
| 23 |
96
| ||
| 115 |
点评：本题主要考查了切线的性质、垂径定理、圆周角定理、内接四边形的性质、等腰三角形的性质、三角函数、勾股定理、相似三角形的判定与性质、三角形的外角性质等知识，综合性比较强，有一定的难度；设FG=3k，然后利用三角函数、相似三角形的性质、等腰三角形的性质等知识求出BC（用k的式子表示）是解决第（3）小题的关键．
练习册系列答案
相关题目
如图，对称轴平行于y轴的抛物线与x轴交于（2，0），（6，0）两点，则它的对称轴为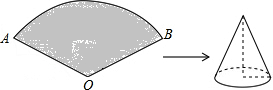
如图所示，已知扇形AOB的半径为6cm，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的全面积为小明在白纸上任意画一个锐角，他画的角在30°到60°之间的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|