题目内容
多项式x4-4y2+4x2+ ,在横杠上填上一个单项式使它能够分解因式并将这个多项式分解因式.
考点:因式分解-分组分解法
专题:
分析:利用完全平方公式以及平方差公式分解得出即可.
解答:解:x4-4y2+4x2+4=(x2-2)2-4y2=(x2-1+2y)(x2-1-2y).
故答案为:4.
故答案为:4.
点评:此题主要考查了分组分解法分解因式,正确分组得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某种植物的主干长出若干数目的支干,每个支干又长出同一数量的小分支,主干、支干和小分支的总数是57,设每个支干长出x个小分支,则可列方程正确的是( )
| A、x2+x(x+1)+x+1=57 |
| B、(x+1)2=57 |
| C、x2+x+1=57 |
| D、x(x+1)=57 |
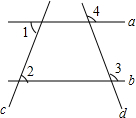 如图,已知:∠1=∠2,∠3=110°,求∠4的度数.
如图,已知:∠1=∠2,∠3=110°,求∠4的度数.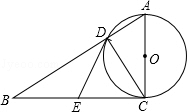 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.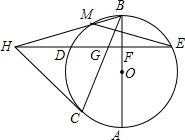 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为
 如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有
如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小方格有