题目内容
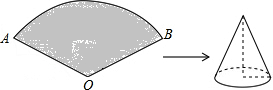 如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为
如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为考点:圆锥的计算
专题:计算题
分析:设圆锥的底面圆的半径为rcm,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=
,解得r=2,然后计算底面积与侧面积的和.
| 120•π•6 |
| 180 |
解答:解:设圆锥的底面圆的半径为rcm,
根据题意得2πr=
,解得r=2,
所以圆锥的全面积=π•22+
•2π•2•6=16π(cm2).
故答案为16πcm2.
根据题意得2πr=
| 120•π•6 |
| 180 |
所以圆锥的全面积=π•22+
| 1 |
| 2 |
故答案为16πcm2.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
 如图,这个几何体从上面看到的平面图形是( )
如图,这个几何体从上面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )| A、8 | B、9 | C、10 | D、8 |
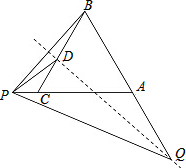 如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.
如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.
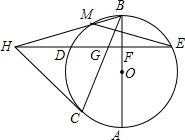 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为