��Ŀ����
11����ͼ1���ڡ�ABC�У���C=90�㣬AC��BC��������CDEF�Ķ���D�ڱ�AC�ϣ���F������CB����CD=x��������CDEF���ABC�ص����ֵ����ΪS��S����x�ĺ���ͼ����ͼ2��ʾ������0��x��m��m��x��2��2��x��nʱ�������Ľ���ʽ��ͬ������1����գ�m��ֵΪ$\frac{3}{2}$��
��2����S����x�ĺ�������ʽ����д��x��ȡֵ��Χ��
��3��S��ֵ�ܷ�Ϊ$\frac{13}{2}$�����ܣ�ֱ��д����ʱx��ֵ�������ܣ�˵�����ɣ�
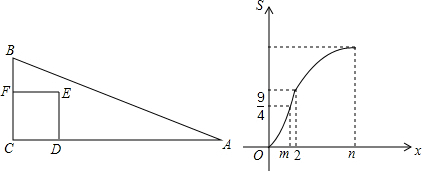
���� ��1����0��x��mʱ�����ͼ�ο�֪S=x2���ѵ㣨m��$\frac{9}{4}$����������m��ֵ��
��2�����ͼ�εı任��֪��m��x��2ʱ����F�˶�����B�������BC����x=mʱ���ɵá�BEF�ס�BAC���������������ε����ʿ����AC�ij�����m��x��2����AB�ֱ�DE��EF�ڵ�P��Q���㣬����x�ֱ��ʾ��PE��QE��S=S������CDEF-S��PEQ���ɵõ�S��x�Ĺ�ϵʽ����2��x��nʱ����AB��DE�ڵ�H������x��ʾ��AP��PH������S=S��ABC-S��APH���ɵõ�S��x�Ĺ�ϵʽ���Ӷ�����ú�������ʽ��
��3�����ã�2��������ù�ϵʽ���ֱ���S=$\frac{13}{2}$������Ӧ�ķ��̽����жϼ��ɣ�
��� �⣺��1����0��x��mʱ����ͼ1��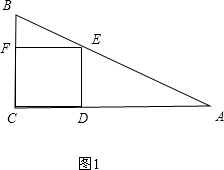
���֪��F��C���˶�����E�˶���AB�ϣ�
��S=x2��
�ߵ㣨m��$\frac{9}{4}$���ں���ͼ���ϣ�
��m2=$\frac{9}{4}$�����m=$\frac{3}{2}$��m=-$\frac{3}{2}$����ȥ����
�ʴ�Ϊ��$\frac{3}{2}$��
��2����$\frac{3}{2}$��x��2ʱ����֪��F��E����AB���˶���B�㣬
��BC=2��
��ͼ1�У���EF��AC��
���BEF�ס�BAC��
��$\frac{BF}{BC}$=$\frac{EF}{AC}$����CF=EF=$\frac{3}{2}$��BF=BC-CF=2-$\frac{3}{2}$=$\frac{1}{2}$��
��$\frac{\frac{1}{2}}{2}$=$\frac{\frac{3}{2}}{AC}$�����AC=6��
�ٵ�0��x��$\frac{3}{2}$ʱ���ɣ�1����֪S=x2��
�ڵ�$\frac{3}{2}$��x��2ʱ����AB�ֱ�DE��EF�ڵ�P��Q���㣬��ͼ2��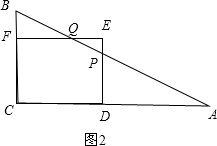
��CD=CF=DE=EF=xʱ��BF=2-x��AD=6-x��
��EF��AC��
��$\frac{BF}{BC}$=$\frac{FQ}{AC}$����$\frac{2-x}{2}$=$\frac{FQ}{6}$��
��FQ=3��2-x����
��QE=EF-FQ=x-3��2-x��=4x-6��
ͬ���ɵ�$\frac{PD}{BC}$=$\frac{AD}{AC}$����$\frac{PD}{2}$=$\frac{6-x}{6}$��
��PD=$\frac{1}{3}$��6-x����
��PE=DE-PD=x-$\frac{1}{3}$��6-x��=$\frac{1}{3}$��4x-6����
��S��PEQ=$\frac{1}{2}$PE•PQ=$\frac{1}{2}$��$\frac{1}{3}$��4x-6��•��4x-6��=$\frac{1}{6}$��4x-6��2��
��S=S������CDEF-S��PEQ=x2-$\frac{1}{6}$��4x-6��2=-$\frac{5}{3}$x2+8x-6��
�۵�2��x��6ʱ������F��B���˶���ʹA��D�غϣ���AB��DE�ڵ�H����ͼ3��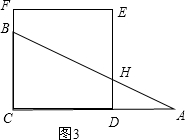
��CD=xʱ����AD=6-x��
ͬ���ɵ�$\frac{DH}{BC}$=$\frac{AD}{AC}$����$\frac{DH}{2}$=$\frac{6-x}{6}$��
��DH=$\frac{1}{3}$��6-x����
��S��ADH=$\frac{1}{2}$DH•AD=$\frac{1}{2}$��$\frac{1}{3}$��6-x��•��6-x��=$\frac{1}{6}$��6-x��2����S��ABC=$\frac{1}{2}$AC•BC=6��
��S=S��ABC-S��APH=6-$\frac{1}{6}$��6-x��2=-$\frac{1}{6}$x2+2x��
���Ͽ�֪S=$\left\{\begin{array}{l}{{x}^{2}��0��x��\frac{3}{2}��}\\{-\frac{5}{3}{x}^{2}+8x-6��\frac{3}{2}��x��2��}\\{-\frac{1}{6}{x}^{2}+2x��2��x��6��}\end{array}\right.$����0��x��6��
��3����S=$\frac{13}{2}$���������������
�ٵ�x2=$\frac{13}{2}$ʱ����x=��$\frac{\sqrt{26}}{2}$����x=-$\frac{\sqrt{26}}{2}$ʱ��Ȼ��������������x=$\frac{\sqrt{26}}{2}$ʱ��$\frac{\sqrt{26}}{2}$��$\frac{3}{2}$��Ҳ������������
�ڵ�-$\frac{5}{3}$x2+8x-6=$\frac{13}{2}$ʱ�������ɵ�10x2-48x+75=0���÷����б�ʽ��=482-4��10��75��0�����÷�����ʵ���⣻
�۵�-$\frac{1}{6}$x2+2x=$\frac{13}{2}$ʱ�������ɵ�x2-12x+39=0���÷����б�ʽ��=122-4��39��0�����÷�����ʵ���⣻
���Ͽ�֪S��ֵ����Ϊ$\frac{13}{2}$��
���� ����Ϊ�ı��ε��ۺ�Ӧ�ã��漰֪ʶ���������ε����ʡ����������ε��ж������ʡ�һԪ���η��̼��������۵ȣ�ȷ�������������˶�����λ�����Ӧ�ĺ���ͼ���ж�Ӧ�ĵ��ǽ���Ĺؼ����ڣ�2������3����ȷ����AC��BC�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ر��ǵڣ�2�����ѶȽϴ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�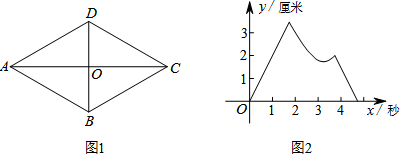
| A�� | ��P��O-A-D-C����Q��O-C-D-O | B�� | ��P��O-A-D-O����Q��O-C-B-O | ||
| C�� | ��P��O-A-B-C����Q��O-C-D-O | D�� | ��P��O-A-D-O����Q��O-C-D-O |
 ��֪�߶�AB=14cm��CΪ�߶�AB����һ�㣬D��AC���е㣬E��CB���е㣬��DE�ij��ȣ�
��֪�߶�AB=14cm��CΪ�߶�AB����һ�㣬D��AC���е㣬E��CB���е㣬��DE�ij��ȣ�