题目内容
19.如图1,四边形ABCD是菱形,对角线AC,BD相交于点O,AB=2厘米,∠BAD=60°.P,Q两点同时从点O出发,以1厘米/秒的速度在菱形的对角线及边上运动.设运动的时间为x秒,P,Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,则P,Q的运动路线可能为( )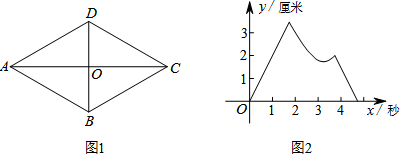
| A. | 点P:O-A-D-C,点Q:O-C-D-O | B. | 点P:O-A-D-O,点Q:O-C-B-O | ||
| C. | 点P:O-A-B-C,点Q:O-C-D-O | D. | 点P:O-A-D-O,点Q:O-C-D-O |
分析 先根据图1中不同路线的位置,判断P,Q间的距离的变换情况,再结合图2中函数图象的变换趋势进行判断分析.
解答 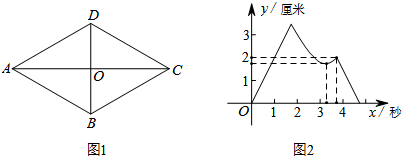 解:∵菱形ABCD中,AB=2,∠BAD=60°
解:∵菱形ABCD中,AB=2,∠BAD=60°
∴AO=CO=$\sqrt{3}$,DO=BO=1
(A)若点P:O-A-D-C,点Q:O-C-D-O,则当x=2+$\sqrt{3}$时,y=0,与图2不符,故(A)错误;
(B)若点P:O-A-D-O,点Q:O-C-B-O,则当x=2$\sqrt{3}$时,y有最大值,当x=$\frac{3}{2}$+$\sqrt{3}$时,y=$\sqrt{3}$,当x=3+$\sqrt{3}$时,y=0,与图2相符,故(B)正确;
(C)当点P与点Q运动完时,点P在点C上,点Q在点O上,所以y=$\sqrt{3}$,与图2不符,故(C)错误;
(D)若点P:O-A-D-O,点Q:O-C-D-O,则当x=2+$\sqrt{3}$时,y=0,与图2不符,故(D)错误.
故选(B)
点评 本题主要考查了动点问题的函数图象以及菱形的性质,用图象分析问题时,要理清图象的含义,即会识图.函数图象是典型的数形结合,通过看图获取图象中关键点所包含的信息,是解决问题的关键.

练习册系列答案
相关题目
10.用加减法解方程组$\left\{\begin{array}{l}{x+y=5}\\{x-y=-1}\end{array}\right.$中,消x用 法,消y用 法.( )
| A. | 加,加 | B. | 加,减 | C. | 减,加 | D. | 减,减 |
7.为了奖励本次竞赛获奖同学,刘老师用280元买了A、B两种纪念品,A种纪念品每个20元,B种纪念品每个60元,且A种纪念品比B种纪念品多买了2个,设买了A种纪念品x个,B种纪念品y个,你认为下列哪一个方程组适合求两种纪念品各买了多少个?( )
| A. | $\left\{\begin{array}{l}{20x+60y=280}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60x+20y=280}\\{x-y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{20x+60y=280}\\{y-x=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60x+20y=280}\\{y-x=2}\end{array}\right.$ |
14.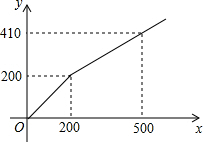 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )| A. | 打八折 | B. | 打七折 | C. | 打六折 | D. | 打五折 |