题目内容
6.如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4$\sqrt{3}$cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).(1)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,则移动时间t=2+$\frac{2}{3}$$\sqrt{3}$.
(2)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围2-$\frac{2}{3}$$\sqrt{3}$<t<2+2$\sqrt{3}$.
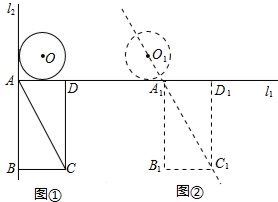
分析 (1)连接OO1,并延长交l2于点E,过点O1作O1F⊥l1于点F,当点O1,A1,C1恰好在同一直线上时,AA1-A1F=O1E;
(2)当d=2时,⊙O与直线AC相切,且直线AC与⊙O相切有两种情况,①当直线AC在⊙O的左边时,AA1+A1F=O1E;②当直线AC在⊙O的右边,AA1-A1F=O1E.
解答 解:(1)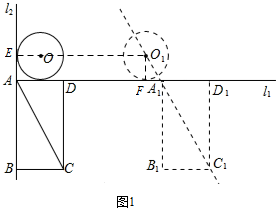 连接OO1,并延长交l2于点E,如图1,
连接OO1,并延长交l2于点E,如图1,
过点O1作O1F⊥l1于点F,
∴由题意知:OO1=3t,AA1=4t,
∵tan∠DAC=$\frac{CD}{AD}=\sqrt{3}$,
∴∠DAC=60°,
∴tan∠O1A1F=$\frac{{O}_{1}F}{{A}_{1}F}$,
∴A1F=$\frac{2}{3}$$\sqrt{3}$,
∵AA1-A1F=O1E,
∴4t-$\frac{2}{3}$$\sqrt{3}$=3t+2,
∴t=2+$\frac{2}{3}\sqrt{3}$;
(2)当d=2时,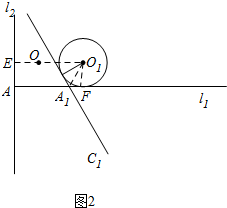
此时⊙O与直线AC相切,
当直线AC在⊙O的左边,如图2,
由(1)可知,A1F=$\frac{2}{3}$$\sqrt{3}$,
∴AA1+A1F=O1E,
∴4t+$\frac{2}{3}$$\sqrt{3}$=3t+2,
∴t=2-$\frac{2}{3}$$\sqrt{3}$,
当直线AC在⊙O的右边,如图3,
此时,A1F=2$\sqrt{3}$
∴AA1-A1F=O1E,
∴4t-2$\sqrt{3}$=3t+2,
∴t=2+2$\sqrt{3}$,
综上所述,当d<2时,t的取值范围为:2-$\frac{2}{3}$$\sqrt{3}$<t<2+2$\sqrt{3}$.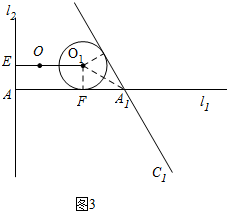
故答案为:(1)2+$\frac{2}{3}\sqrt{3}$;(2)2-$\frac{2}{3}$$\sqrt{3}$<t<2+2$\sqrt{3}$.
点评 本题考查圆的综合问题,涉及切线的性质,锐角三角函数,解方程等知识,内容较为综合,考查学生灵活运用知识的能力.

 计算高手系列答案
计算高手系列答案 已知:如图,线段AD=10cm,AC=BD=7cm,E,F分别是AB,CD的中点,求EF的长.
已知:如图,线段AD=10cm,AC=BD=7cm,E,F分别是AB,CD的中点,求EF的长.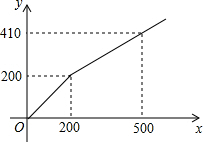 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )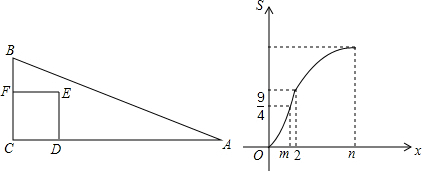
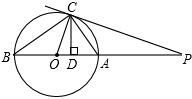 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.