题目内容
3.解方程与不等式组:(1)解方程组$\left\{\begin{array}{l}x+y=-1\\ x-2y=5.\end{array}$
(2)解不等式组$\left\{\begin{array}{l}3x+1<2(x+2)\\-\frac{x}{3}≤\frac{5x}{3}+2.\end{array}$.
分析 (1)利用消元法,由①-②消除x从而求得x,然后将x的值代入方程即可求解;
(2)分别解得不等式①②,然后求得他们的公共部分即可求解.
解答 解:(1)∵方程组$\left\{\begin{array}{l}{x+y=-1①}\\{x-2y=5②}\end{array}\right.$,
∴由①-②得:3y=-6,解得y=-2,
∴把y=-2代入①得:x=1,
∴方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
(2)∵不等式组$\left\{\begin{array}{l}{3x+1<2(x+2)①}\\{-\frac{x}{3}≤\frac{5x}{3}+2②}\end{array}\right.$,
∴解①得:x<3,解②得x≥-1,
∴不等式组的解集为:-1≤x<3.
点评 本题主要考查了解一元一次不等式组以及解二元一次方程组的知识,解题的关键是掌握解不等式得步骤以及熟练掌握加减消元法解方程组,此题难度不大.

练习册系列答案
相关题目
13.在早餐店里,王伯伯买5个馒头,3个包子,老板少收2元,只要5元.李太太买了11个馒头,5个包子,老板以售价的九折优惠,只要9元.若设馒头每个x元,包子每个y元,则下列哪一个二元一次方程组可表示题目中的数量关系?( )
| A. | $\left\{\begin{array}{l}{5x+3y=5+2}\\{11x+5y=9×0.9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+3y=5+2}\\{11x+5y=9÷0.9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+3y=5-2}\\{11x+5y=9×0.9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+3y=5-2}\\{11x+5y=9÷0.9}\end{array}\right.$ |
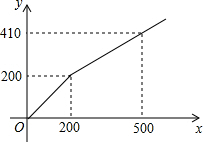 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
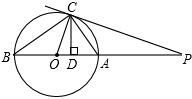 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.