题目内容
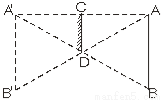
已知在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B',如图所示,则与线段BC相等的线段是____，与线段AB相等的线段是_______和_______,与∠B相等的角是________和_______,因此可得到∠B=________.
B′ C AB′ BB ′ ∠B′ ∠BAB′ 60°
【解析】∵以直线AC为对称轴,点B的对称点是B' ，
∴B′C=BC ， ∠B′CA=∠BCA=90°，AB′=AB=2BC，
∴AB′=AB=BB′，
∴∠B′=∠B=∠B′AB =60°.
练习册系列答案
相关题目
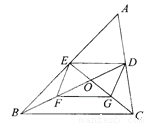
已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．
证明见解析.
【解析】试题分析：根据BD，CE是△ABC的中线可得DE是△ABC的中位线，F，G分别是OB，OC的中点可得FG是△BOC的中位线，根据三角形中位线定理可得DE∥BC且DE=BC，FG∥BC且FG=BC，进而可得DE∥FG且DE=FG，根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析：∵BD、CE是△ABC的中线，∴DE是△ABC的中位线，
∴DE∥B... 用四块如图所示的两色正方形瓷砖，拼成一个新的正方形，使拼成轴对称图案，请至少给出三种不同的拼法：
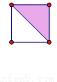
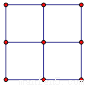
见解析
【解析】根据轴对称的概念进行图形设计即可.
【解析】
根据轴对称要求，设计出利用两色磁砖拼成的正方形如图所示. 如图，将一个等腰直角三角形按图示方式依次翻折，则下列说法正确的个数有（ ）
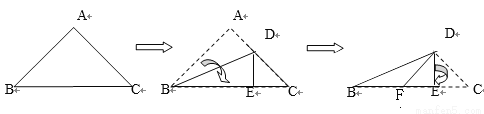
①DF平分∠BDE；②△BFD是等腰三角形；③△CED的周长等于BC的长
A. 1个 B. 2个 C. 3个 D. 0个
B
【解析】根据轴对称的性质即可得出答案.
【解析】
由多次翻折可得，∠DBE=∠ABD=∠ABC=×45°=22.5°，
∠CDE =90°－∠C =90°－45°=45°=∠C，
∠FDE=∠CDE =45°，
∴∠ABD=∠EDB=∠ADE=×(180°－∠CDE) =×(180°－45°)=67. 5°，
∴①DF平分∠BDE错误，如果正确的话，∠BD... 小红想在卧室放一穿衣镜，能看到自己的全身像，那么她至少应买多高(宽度适当)的穿衣镜？
镜高至少为身高的一半
【解析】试题分析：设小红用线段AB表示，则A头部，通过镜子下沿D处可以看到自己的脚的映像，而根据轴对称的性质，可以通过镜子顶端C处看到自己的头部映像，因此，镜子调试至少需要自己身体的一半高度.
【解析】
由轴对称的性质得CA=CA′，
∵CD∥AB,
∴CD为△AA′B的中位线 ，
∴镜子高度至少为身高的一半． 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 如果一个三角形是轴对称图形，且有一个内角是60°,那么这个三角形是( )
A. 等边三角形 B. 等腰直角三角形 C. 等腰三角形 D. 含30°角的直角三角形
A
【解析】∵这个三角形是轴对称图形 ，
∴一定有两个角相等，
∴这是一个等腰三角形.
∵有一个内角是60°，
∴这个三角形是等边三角形.
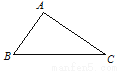
故选A. 如图,已知△ABC，别以A、C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连结AD，CD，则有( )
A. ∠ADC与∠BAD相等 B. ∠ADC与∠BAD互补
C. ∠ADC与∠ABC互补 D. ∠ADC与∠ABC互余
B
【解析】如图，依题意得AD=BC、CD=AB，∴四边形ABCD是平行四边形，∴∠ADC+∠BAD=180°，∠ADC=∠ABC，∴B正确． 计算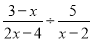 
=_____________
【解析】试题解析：
故答案为：