题目内容
如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A. 等边三角形 B. 等腰直角三角形 C. 等腰三角形 D. 含30°角的直角三角形
 A
【解析】∵这个三角形是轴对称图形 ,
∴一定有两个角相等,
∴这是一个等腰三角形.
∵有一个内角是60°,
∴这个三角形是等边三角形.
故选A.
A
【解析】∵这个三角形是轴对称图形 ,
∴一定有两个角相等,
∴这是一个等腰三角形.
∵有一个内角是60°,
∴这个三角形是等边三角形.
故选A.
如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 度.
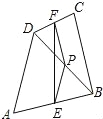
 18.
【解析】
试题分析:根据中位线定理和已知,易证明△EPF是等腰三角形.∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=18°,∴∠PEF=∠PFE=18°.故答案为:18.
18.
【解析】
试题分析:根据中位线定理和已知,易证明△EPF是等腰三角形.∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=18°,∴∠PEF=∠PFE=18°.故答案为:18. 下列说法中,正确的是( )
A. 两个全等三角形,一定是轴对称的
B. 两个轴对称的三角形,一定是全等的
C. 三角形的一条中线把三角形分成以中线为轴对称的两个图形
D. 三角形的一条高把三角形分成以高线为轴对称的两个图形
 B
【解析】根据轴对称图形的概念对各选项分析判断即可得解.
【解析】
A. 两个全等三角形,一定是轴对称的错误,三角形全等位置上不一定关于某一直线对称,故本选项错误;
B. 两个轴对称的三角形,一定全等,正确;
C. 三角形的一条中线把三角形分成以中线为轴对称的两个图形,错误;
D. 三角形的一条高把三角形分成以高线为轴对称的两个图形,错误.
故选B.
...
B
【解析】根据轴对称图形的概念对各选项分析判断即可得解.
【解析】
A. 两个全等三角形,一定是轴对称的错误,三角形全等位置上不一定关于某一直线对称,故本选项错误;
B. 两个轴对称的三角形,一定全等,正确;
C. 三角形的一条中线把三角形分成以中线为轴对称的两个图形,错误;
D. 三角形的一条高把三角形分成以高线为轴对称的两个图形,错误.
故选B.
... 已知在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B',如图所示,则与线段BC相等的线段是____,与线段AB相等的线段是_______和_______,与∠B相等的角是________和_______,因此可得到∠B=________.

 B′ C AB′ BB ′ ∠B′ ∠BAB′ 60°
【解析】∵以直线AC为对称轴,点B的对称点是B' ,
∴B′C=BC , ∠B′CA=∠BCA=90°,AB′=AB=2BC,
∴AB′=AB=BB′,
∴∠B′=∠B=∠B′AB =60°.
B′ C AB′ BB ′ ∠B′ ∠BAB′ 60°
【解析】∵以直线AC为对称轴,点B的对称点是B' ,
∴B′C=BC , ∠B′CA=∠BCA=90°,AB′=AB=2BC,
∴AB′=AB=BB′,
∴∠B′=∠B=∠B′AB =60°. 已知互不平行的两条线段AB,CD关于直线l对称,AB,CD所在直线交于点P,下列结论中:①AB=CD;②点P在直线l上; ③若A、C是对称点,则l垂直平分线段AC; ④若B、D是对称点,则PB=PD.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
 D
【解析】由抽对称的性质知,①②③④都正确.
故选D.
D
【解析】由抽对称的性质知,①②③④都正确.
故选D. 下列说法正确的是( )
A. 两个全等的三角形一定关于某条直线对称 B. 关于某条直线的对称的两个三角形一定全等
C. 直角三角形是轴对称图形 D. 锐角三角形都是轴对称图形
 B
【解析】A.根据轴对称的定义,全等三角形不一定关于某直线对称,故错误;
B. 根据轴对称的性质,关于某条直线的对称的两个三角形一定全等,故正确;
C.直角三角形中,等腰直角三角形是轴对称图形,其它一般的直角三角形不是,故错误;
D.锐角三角形不一定是轴对称图形,如三个角分别是50°、60°、70°的三角形就不是轴对称图形,故错误.
故选B.
B
【解析】A.根据轴对称的定义,全等三角形不一定关于某直线对称,故错误;
B. 根据轴对称的性质,关于某条直线的对称的两个三角形一定全等,故正确;
C.直角三角形中,等腰直角三角形是轴对称图形,其它一般的直角三角形不是,故错误;
D.锐角三角形不一定是轴对称图形,如三个角分别是50°、60°、70°的三角形就不是轴对称图形,故错误.
故选B. 如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,CD∥AF,请你添加一个条件:_________使四边形ABCD是平行四边形
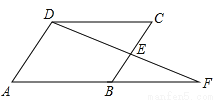
 AB=BF
【解析】添加条件是AB=BF,求出∠CDE=∠F,CE=BE,根据AAS证△CDE≌△BFE,推出DC=BF,推出AB=CD,CD∥AB,根据平行四边形的判定推出即可.
AB=BF
【解析】添加条件是AB=BF,求出∠CDE=∠F,CE=BE,根据AAS证△CDE≌△BFE,推出DC=BF,推出AB=CD,CD∥AB,根据平行四边形的判定推出即可. 下列判断正确的是( )
A. 一组对边平行,另一组对边相等的四边形一定是平行四边形
B. 两条对角线互相平分的四边形一定是平行四边形
C. 两组邻角分别互补的四边形一定是平行四边形
D. 两条对角线相等的四边形一定是平行四边形
 B
【解析】解:A.一组对边平行,另一组对边相等的四边形不一定是平行四边形,例如:等腰梯形,故本选项错误;
B.两条对角线互相平分的四边形是平行四边形,故本选项正确;
C.两组邻角分别互补的四边形不一定是平行四边形,还可能是梯形,故本选项错误;
D.两条对角线相等的四边形不一定是平行四边形,例如:等腰梯形的两条对角线相等,故本选项错误;
故选B.
B
【解析】解:A.一组对边平行,另一组对边相等的四边形不一定是平行四边形,例如:等腰梯形,故本选项错误;
B.两条对角线互相平分的四边形是平行四边形,故本选项正确;
C.两组邻角分别互补的四边形不一定是平行四边形,还可能是梯形,故本选项错误;
D.两条对角线相等的四边形不一定是平行四边形,例如:等腰梯形的两条对角线相等,故本选项错误;
故选B. 计算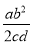 ÷
÷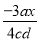 的结果是( )
的结果是( )
A. -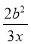 B.
B. 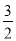 b2x C.
b2x C. 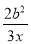 D. -
D. -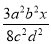
 A
【解析】试题解析: ,故答案是A选项.
故选A.
A
【解析】试题解析: ,故答案是A选项.
故选A. 
