题目内容
1.如图①,在边长为4cm的正方形ABCD中,点P以每秒2cm的速度从点A出发,沿AB→BC的路径运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动2.5秒时,PQ的长是( )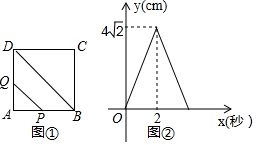
| A. | $2\sqrt{2}cm$ | B. | $3\sqrt{2}cm$ | C. | $4\sqrt{2}cm$ | D. | $5\sqrt{2}cm$ |
分析 根据运动速度乘以时间,可得PQ的长,根据线段的和差,可得CP的长,根据勾股定理,可得答案.
解答 解:点P运动2.5秒时P点运动了5cm,
CP=8-5=3cm,
由勾股定理,得
PQ=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$cm,
故选:B.
点评 本题考查了动点函数图象,利用勾股定理是解题关键.

练习册系列答案
相关题目
13.分式方程$\frac{x}{x-1}$-$\frac{2}{x}$=1的解为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=2或 x=3 |
10.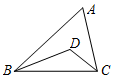 如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
 如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )
如图,△ABC中,∠A=60°,BD,CD分别是∠ABC,∠ACB的平分线,则∠BDC的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
11.某同学家长应邀参加孩子就读中学的开放日活动,他打算上午随机听一节孩子所在1班的课,下表是他拿到的当天上午1班的课表,如果每一节课被听的机会均等,那么他听数学课的概率是$\frac{1}{4}$.
| 班级 节次 | 1班 |
| 第1节 | 语文 |
| 第2节 | 英语 |
| 第3节 | 数学 |
| 第4节 | 音乐 |
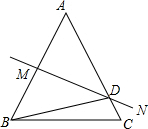 如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为14cm.
如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为14cm.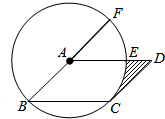 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若$\widehat{EF}$的长为π,则图中阴影部分的面积为8-2π.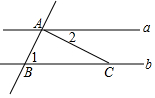 如图,a∥b,AB⊥AC,∠1=65°29′,则∠2=24°31′.
如图,a∥b,AB⊥AC,∠1=65°29′,则∠2=24°31′.