题目内容
6.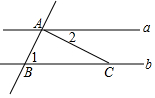 如图,a∥b,AB⊥AC,∠1=65°29′,则∠2=24°31′.
如图,a∥b,AB⊥AC,∠1=65°29′,则∠2=24°31′.
分析 先根据平行线的性质,得出∠1+∠BAC+∠2=180°,再根据AB⊥AC,即可得到∠2.
解答 解:∵a∥b,AB⊥AC,
∴∠1+∠BAC+∠2=180°,
即65°29′+90°+∠2=180°,
∴∠2=24°31′,
故答案为:24°31′.
点评 本题主要考查了平行线的性质的运用以及垂线的定义的运用,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
1.如图①,在边长为4cm的正方形ABCD中,点P以每秒2cm的速度从点A出发,沿AB→BC的路径运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动2.5秒时,PQ的长是( )
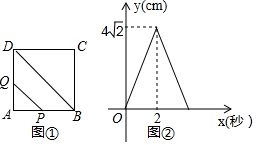

| A. | $2\sqrt{2}cm$ | B. | $3\sqrt{2}cm$ | C. | $4\sqrt{2}cm$ | D. | $5\sqrt{2}cm$ |
11.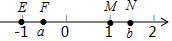 如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
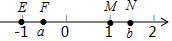 如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
16.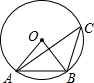 如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那么∠ACB的度数是( )
如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那么∠ACB的度数是( )
 如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那么∠ACB的度数是( )
如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,如果∠AOB=64°,那么∠ACB的度数是( )| A. | 26° | B. | 30° | C. | 32° | D. | 64° |
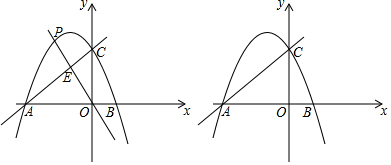
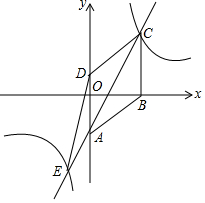 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.
已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b. 学完一元一次不等式的解法后,老师布置了如下练习:
学完一元一次不等式的解法后,老师布置了如下练习: