题目内容
18. △ABC中,AD⊥BC,垂足为D,作DE⊥AB,DF⊥AC,连结EF,求证:∠ABC=∠AFE.
△ABC中,AD⊥BC,垂足为D,作DE⊥AB,DF⊥AC,连结EF,求证:∠ABC=∠AFE.
分析 由垂线的定义得出∠ADB=90°,∠DEA=90°,由角的互余关系得出∠ABC=∠ADE,再证明A、E、D、F四点共圆,由圆周角定理得出∠AFE=∠ADE,即可得出∠ABC=∠AFE.
解答 证明:如图所示:
∵AD⊥BC,DE⊥AB,
∴∠ADB=90°,∠DEA=90°,
∴∠ABC+∠BAD=90°,∠BAD+∠ADE=90°,
∴∠ABC=∠ADE,
∵DF⊥AC,
∴∠DFA=90°,
∴∠DEA+∠DFA=180°,
∴A、E、D、F四点共圆,
∴∠AFE=∠ADE,
∴∠ABC=∠AFE.
点评 本题是四点共圆题目,考查了四点共圆、圆周角定理、垂线的定义、角的互余关系等知识;本题综合性强,难度适中,证明四点共圆是解决问题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
6.从正方形铁片的一边截去2cm宽的一条长方形铁片,再从剩余部分的短边截去3cm宽的一条长方形铁片,余下的面积是42cm2,则原来的正方形铁片的面积是( )
| A. | 6cm2 | B. | 16cm2 | C. | 64cm2 | D. | 81cm2 |
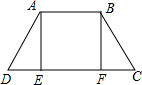 如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么?
如图所示,四边形ABCD是一条河堤坝的横截面,AE=BF,且AE⊥CD,BF⊥CD,垂足分别为E、F,AD=BC,∠C与∠D是否相等?为什么? 分别以?ABCD的各边为边,向形外作四个正方形,试说明依次连接这四个正方形对角线的交点所构成的四边形是正方形.
分别以?ABCD的各边为边,向形外作四个正方形,试说明依次连接这四个正方形对角线的交点所构成的四边形是正方形. 如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.
如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$. 甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.