题目内容
12.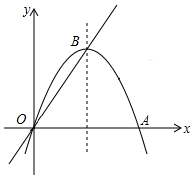 如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
分析 先根据抛物线与x轴的交点问题得到A(6,0),则抛物线的对称轴为直线x=3,则可确定B(3,4),利用勾股定理可计算出BO=BA=5,作点M关于直线x=3的对称点M′,直线x=3与x轴的交点为C,如图,利用BA与BO关于BC对称得到点M′在BA上,则ON+MN=ON+M′N,接着利用两点之间线段最短和垂线段最短可得当点O、N、M′共线且垂直AB时,ON+M′N最短,然后利用面积法求出垂线段OM′的长即可.
解答 解: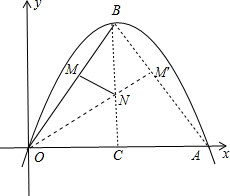 令y=0,ax2-6ax=0,解得x1=0,x2=6,则A(6,0),
令y=0,ax2-6ax=0,解得x1=0,x2=6,则A(6,0),
所以抛物线的对称轴为直线x=3,
当x=3时,y=$\frac{4}{3}$x=4,则B(3,4),
所以BO=BA=5,
作点M关于直线x=3的对称点M′,直线x=3与x轴的交点为C,如图,
因为BA与BO关于BC对称,
所以点M′在BA上,则ON+MN=ON+M′N,
所以当点O、N、M′共线且垂直AB时,即OM′⊥AB,ON+M′N最短,最短长度为垂线段OM′的长,
而$\frac{1}{2}$OM′•AB=$\frac{1}{2}$BC•OA,
所以OM′=$\frac{24}{5}$,
即ON+MN的最小值为$\frac{24}{5}$.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
4.下列四个几何体:
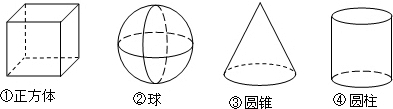
其中左视图与俯视图相同的几何体共有( )

其中左视图与俯视图相同的几何体共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.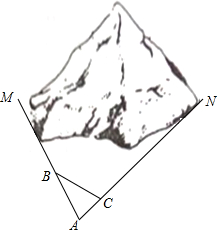 (1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(2)列方程(组)或不等式(组)解应用题:
2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%,求这份快餐最多含有多少克的蛋白质?
 (1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
(1)如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.(2)列方程(组)或不等式(组)解应用题:
2015年的5月20日是第15个中国学生营养日,我市某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如表).
| 信息 1、快餐成分:蛋白质、脂肪、碳水化合物和其他 2、快餐总质量为400克 3、碳水化合物质量是蛋白质质量的4倍 |

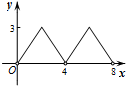
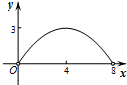
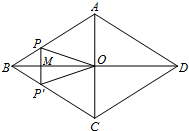 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )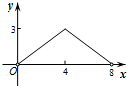
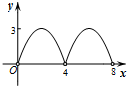
 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )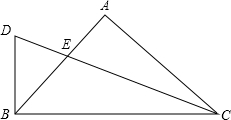 如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.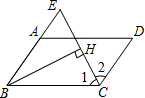 在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.