题目内容
2.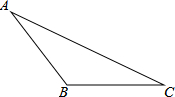 如图,在△ABC中画出高线AD、中线BE、角平分线CF.
如图,在△ABC中画出高线AD、中线BE、角平分线CF.
分析 根据三角形的中线、高和角平分线的概念、运用基本尺规作图过点A作BC的垂线交CB的延长线于D,作出AC的中点E,连接BE,作∠C的平分线交AB于点F,则AD、BE、CF即为所求.
解答 解:如图,AD为高线,BE为中线,CF为角平分线.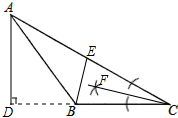
点评 本题考查的是复杂作图,掌握基本尺规作图、理解三角形的中线、高和角平分线的概念是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
5.计算(-xy3)2的结果是( )
| A. | x2y6 | B. | -x2y6 | C. | x2y9 | D. | -x2y9 |
13.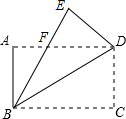 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
(1)求证:△EDF≌△ABF;
(2)∠ABF=30°,AB=2$\sqrt{3}$,求△BDF的面积.
 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.(1)求证:△EDF≌△ABF;
(2)∠ABF=30°,AB=2$\sqrt{3}$,求△BDF的面积.
17.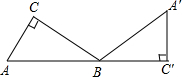 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
12. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的平均速度为每分钟70米 | |
| C. | 小明在上述过程中所走的路程为6600米 | |
| D. | 小明休息前爬山的平均速度大于休息后爬山的平均速度 |
 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间. 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )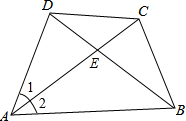 四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.