题目内容
10.某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
分析 (1)先列表展示所有3种等可能的结果数,再找出总额是30元所占结果数,然后根据概率公式计算;
(2)找出总额超过51元的结果数,然后根据概率公式计算.
解答 解:(1)列表:
共有3种等可能的结果数,其中总额是30元占1种,
所以取出纸币的总额是30元的概率=$\frac{1}{3}$;
(2)共有3种等可能的结果数,其中总额超过51元的有2种,
所以取出纸币的总额可购买一件51元的商品的概率为$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
1.已知圆的半径是2$\sqrt{3}$,则该圆的内接正六边形的面积是( )
| A. | 3$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
5.计算(-xy3)2的结果是( )
| A. | x2y6 | B. | -x2y6 | C. | x2y9 | D. | -x2y9 |
6.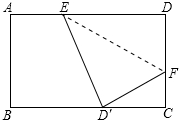 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )