题目内容
6.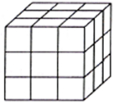 如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;(1)只有一面涂有颜色的概率;
(2)至少有两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
分析 (1)得出一面涂有颜色的小正方体有6个,再根据概率公式解答即可;
(2)得出至少有两面涂有颜色的小正方体有20个,再根据概率公式解答即可;
(3)得出各个面都没有涂颜色的小正方体共有1个,再根据概率公式解答即可.
解答 解:(1)因为一面涂有颜色的小正方体有6个,
所以P(一面涂有颜色)=$\frac{6}{27}$=$\frac{2}{9}$;
(2)因为至少两面涂有颜色的小正方体有12+8个,
所以P(至少两面涂有颜色)=$\frac{12+8}{27}$=$\frac{20}{27}$;
(3)因为各个面都没有涂颜色的小正方体共有1个,
所以P(各个面都没有涂颜色)=$\frac{1}{27}$.
点评 此题主要考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.关键是找到相应的具体数目.

练习册系列答案
相关题目
16.某花卉基地种植了郁金香和玫瑰两种花卉共30亩,有关数据如表:
(1)设种植郁金香x亩,两种花卉总收益为y万元,求y关于x的函数关系式.(收益=销售额-成本)
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
| 成本 (单位:万元/亩) | 销售额 (单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的成本的总额不超过70万元,要使获得的收益最大,基地应种植郁金香和玫瑰个多少亩?
17.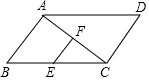 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )| A. | 2.5 | B. | 5 | C. | 10 | D. | 15 |
11.三角形的两边长分别为4和9,则它的第三边长可以为( )
| A. | 4 | B. | 5 | C. | 9 | D. | 13 |
18. 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )| A. | 44° | B. | 46° | C. | 88° | D. | 54° |
15. 某中学九年级学生进行了五次体育模拟测试,甲同学的测试
某中学九年级学生进行了五次体育模拟测试,甲同学的测试
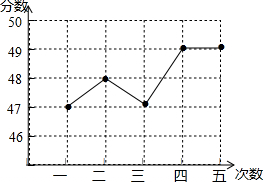
成绩如表,乙同学的测试成绩折线统计图如图所示:
(1)请根据甲、乙两同学五次体育模拟测试的成绩填写下表:
(2)在图中用虚线画出甲测试成绩的折线统计图;
(3)甲、乙两位同学在这五次体育模拟测试中,谁的成绩较为稳定?谁的成绩一直呈上升趋势.
 某中学九年级学生进行了五次体育模拟测试,甲同学的测试
某中学九年级学生进行了五次体育模拟测试,甲同学的测试成绩如表,乙同学的测试成绩折线统计图如图所示:
| 次 数 | 一 | 二 | 三 | 四 | 五 |
| 分 数 | 46 | 47 | 48 | 49 | 50 |
| 中位数 | 平均数 | 方差 | |
| 甲 | 48 | 48 | 2 |
| 乙 | 48 | 48 | 0.8 |
(3)甲、乙两位同学在这五次体育模拟测试中,谁的成绩较为稳定?谁的成绩一直呈上升趋势.
16.下面是某一天永州市11个旅游景区最高气温(单位:℃)的统计表:
则下列说法正确的是( )
| 景区 | 潇水湖 | 东山景区 | 浯溪碑林 | 舜皇山 | 阳明山 | 鬼崽岭 | 九嶷山 | 上甘棠 | 涔天河 | 湘江源 | 南武当 |
| 气温 | 31 | 30 | 31 | 25 | 28 | 27 | 26 | 28 | 28 | 25 | 29 |
| A. | 该组数据的方差为0 | B. | 该组数据的平均数为25 | ||
| C. | 该组数据的中位数为27 | D. | 该组数据的众数为28 |