题目内容
11.三角形的两边长分别为4和9,则它的第三边长可以为( )| A. | 4 | B. | 5 | C. | 9 | D. | 13 |
分析 设它的第三边长为x,根据三角形的三边关系可得9-4<x<9+4,再解即可得到第三边的范围,进而可得答案.
解答 解:设它的第三边长为x,由题意得:
9-4<x<9+4,
5<x<13,
故选:C.
点评 此题主要考查了三角形的三边关系,关键是掌握任意两边之和>第三边,任意两边之差<第三边.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
1.某校有15名同学参加某比赛,预赛成绩各不相同,取前8名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这15名同学成绩的( )
| A. | 最高分 | B. | 中位数 | C. | 方差 | D. | 平均数 |
2.已知$\frac{x}{3}$-$\frac{y}{2}$=1,用含x的代数式表示y正确的是( )
| A. | y=$\frac{2}{3}$x-2 | B. | x=$\frac{3y+1}{2}$ | C. | y=$\frac{2x-1}{3}$ | D. | y=-$\frac{1}{3}$-$\frac{2}{3}$x |
19. 如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
 如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )
如图,直线y=x+b与直线y=kx+b交于点P(3,5),则关于x的不等式x+b>kx+6的解集是( )| A. | x>3 | B. | x<3 | C. | x≥3 | D. | x≤3 |
16. 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )
 如图,AB∥CD,若∠1=40°,则∠2的度数为( )
如图,AB∥CD,若∠1=40°,则∠2的度数为( )| A. | 40° | B. | 150° | C. | 140° | D. | 130° |
3.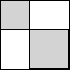 如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
 如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )
如图,利用两个正方形和两个长方形拼成一个大正方形,已知两个正方形的边长分别为3cm和4cm,将一个骰子任意抛向大正方形,落在白色区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{24}{49}$ | D. | $\frac{25}{49}$ |
1.-3的绝对值是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $-\frac{1}{3}$ | D. | -3 |
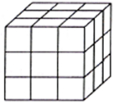 如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;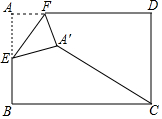 如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.
如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是$\sqrt{10}$-1.