题目内容
1.A、B两地相距35km,甲8:00由A地出发骑自行车去B地,平均速度为12km/h;乙10:00由A地出发乘汽车也去B地,平均速度为60km/h.(1)分别写出两个人行程关于时刻的函数解析式;
(2)乙能否在途中超过甲?如果能超过,何时超过?
分析 (1)根据行程=速度×时间分别列式即可;
(2)利用60(x-10)>12(x-8),进而得出x的取值范围,进而得出答案.
解答 解:(1)设行程为ykm,时间为xh,
甲:y=12(x-8)=12x-96,
乙:y=60(x-10)=60x-600;
(2)能在途中超过甲,
理由:由60(x-10)>12(x-8),
解得:x>10.5,
此时60(10.5-10)=30<35,
答:10:30后乙超过甲.
点评 本题考查了一次函数的应用,主要利用了函数解析式的求解,理解并表示出时间是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.甲、乙、丙三地海拔高度分别为-100米、-300米、500米,那么最高的地方比最低的地方高( )
| A. | 400米 | B. | 600米 | C. | 200米 | D. | 800米 |
 如图是由 4 个边长为 1 的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为 $\sqrt{5}$的平行四边形的个数是( )
如图是由 4 个边长为 1 的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为 $\sqrt{5}$的平行四边形的个数是( )

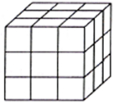 如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;
如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成27个大小相同的小正方体,从这些小正方体中任意取出一个,求取出的小正方体;