题目内容
15．
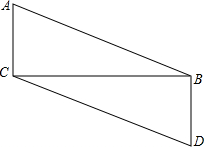已知：如图，AC⊥CB，BD⊥BC，AB=DC．求证：AB∥CD．
分析 根据垂直的定义得出△ACB和△DBC是直角三角形，再根据HL证明△ACB≌△DBC，得出∠ABC=∠DCB，根据内错角相等，两直线平行证明即可．
解答 证明：∵AC⊥CB，BD⊥BC，
∴∠ACB=∠DBC=90°，
在Rt△ACB和Rt△DBC中，
$\left\{\begin{array}{l}{AB=CD}\\{BC=CB}\end{array}\right.$，
∴Rt△ACB≌Rt△DBC（HL），
∴∠ABC=∠DCB，
∴AB∥CD．
点评 本题考查了全等三角形的判定与性质的运用，解答时证明三角形全等是关键．
练习册系列答案
阅读快车系列答案
相关题目
5．为了准备学校秋季田径运动会，我校学生小林进行了刻苦的训练，下表为他一周的跑步变化情况，（“+”表示增加，“-”表示减少）小林在上周的星期日跑步为400米．
（1）请问本周哪天跑步训练量最多？哪天跑步训练量最少？分别是多少？
（2）若上周平均每日跑490米，则本周跑步训练的总量比上周上升还是下降了多少米？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 跑步训练量与前一天相比变化情况（米） | +100 | -20 | +50 | +20 | -35 | +15 | -9 |
（2）若上周平均每日跑490米，则本周跑步训练的总量比上周上升还是下降了多少米？
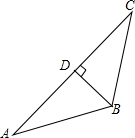如图，在△ABC中，BD⊥AC于点D，若BC=10，AC=20，∠C=37°，求AB的长．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
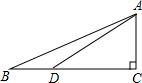如图，AC⊥BC，cos∠ADC=$\frac{4}{5}$，tanB=$\frac{{\sqrt{3}}}{3}$，AD=10，求：（1）AC的长；（2）BD的长．
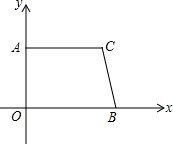如图，在直角梯形AOBC中，AC∥OB，且OB=6，AC=5，OA=4．