题目内容
3.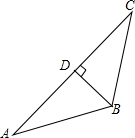 如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 根据∠C的正弦和正切求得BD,CD,再得出AD,根据勾股定理得出AB的长.
解答 解:∵BD⊥AC,
∴∠BDC=∠BDA=90°,
∵sinC=$\frac{BD}{BC}$,tanC=$\frac{BD}{CD}$,
∴BD=BC•sinC,CD=$\frac{BD}{tanC}$,
∵BC=10,AC=20,
∴BD=10×0.6=6,CD=$\frac{6}{0.75}$=8,
∵AC=20,
∴AD=20-8=12,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{52}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.一根长80cm的弹簧,一端固定.如果另一端挂上物体,那么在正常情况下物体的质量每增加1kg可使弹簧增长2cm.
(1)正常情况下,当挂着xkg的物体时,弹簧的长度是多少厘米?
(2)利用(1)的结果,完成下表:
(1)正常情况下,当挂着xkg的物体时,弹簧的长度是多少厘米?
(2)利用(1)的结果,完成下表:
| 物体的质量/kg | 1 | 2 | 3 | 4 |
| 弹簧的长度/cm | 82 | 84 | 86 | 88 |
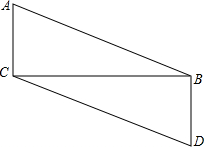 已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD.
已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD.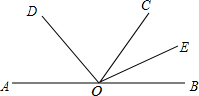 如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数.
如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数. 如图所示,已知AC平分∠DAB,且∠DAC=∠DCA.
如图所示,已知AC平分∠DAB,且∠DAC=∠DCA.