题目内容
4.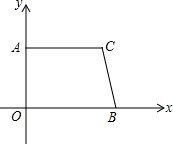 如图,在直角梯形AOBC中,AC∥OB,且OB=6,AC=5,OA=4.
如图,在直角梯形AOBC中,AC∥OB,且OB=6,AC=5,OA=4.(1)直接写出B、C两点的坐标;
(2)以O、A、B、C中的三点为顶点可组成哪几个不同的三角形?
(3)是否在边AC和BC(含端点)上分别存在点M和点N,使得△MON的面积最大时,它的周长还最短?若存在,请说明理由,并求出这时点M、N的坐标;若不存在,为什么?
分析 (1)由OB=6,点B在x轴,得到B点的坐标,根据AC∥OB,AC=5,得到点C的坐标;
(2)根据不在同一直线的三点能组成一个三角形,得到以O、A、B、C中的三点为顶点可组成4个不同的三角形;
(3)过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,则S△MON=S△OMP+S△NMP=$\frac{1}{2}$MP•QG+$\frac{1}{2}$MP•GN,因为QN、MP同时取得最大值是OB、OA,所以M应该和A重合,从而求得M的坐标.
解答 解:(1)∵OB=6,OA=4,
∴B(6,0)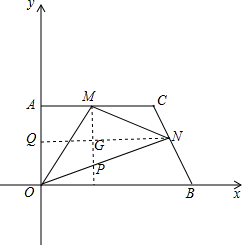
∵AC∥OB,AC=5,
∴C(5,4);
(2)以O、A、B、C中的三点为顶点可组成的三角形为△AOB△AOC△BOC△ABC四个不同的三角形;
(3)如图,过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,
则S△MON=S△OMP+S△NMP=$\frac{1}{2}$MP•QG+$\frac{1}{2}$MP•GN,
∵MP≤OA,QN≤OB,
∴当点N与点B重合,M在AC上运动时,QN,MP同时取得最大值BO,OA,
∴△MON的面积=$\frac{1}{2}$OA•OB,
∴M点与A点重合,
∴M(0,4),△MON的周长=10+$\sqrt{56}$,
当△OMN是等腰三角形时,点N与B重合,
则OM=MN,∴M(3,4),
∴△MON的面积=$\frac{1}{2}$OA•OB,
∴△MON的周长=16<10+$\sqrt{56}$,
∴存在点M和点N,使得△MON的面积最大时,它的周长还最短,
M(3,4).
点评 本题考查了直角梯形的性质,坐标和图形的性质,轴对称的性质,不在同一直线的三点能组成一个三角形等知识点,作出辅助线是本题的关键.

 阅读快车系列答案
阅读快车系列答案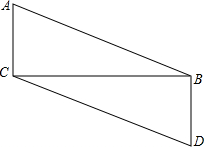 已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD.
已知:如图,AC⊥CB,BD⊥BC,AB=DC.求证:AB∥CD.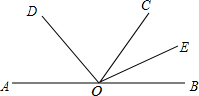 如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数.
如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数.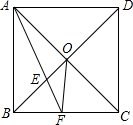 如图,已知正方形ABCD边长为2,AF平分∠BAC,求OF的长.
如图,已知正方形ABCD边长为2,AF平分∠BAC,求OF的长.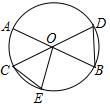 如图,AB、CD为⊙O的直径,$\widehat{AC}$=$\widehat{CE}$,求证:BD=CE.
如图,AB、CD为⊙O的直径,$\widehat{AC}$=$\widehat{CE}$,求证:BD=CE. 如图所示,已知AC平分∠DAB,且∠DAC=∠DCA.
如图所示,已知AC平分∠DAB,且∠DAC=∠DCA.