题目内容
4.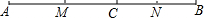 如图,点C在线段AB上,点M.N分别是AC、BC的中点.
如图,点C在线段AB上,点M.N分别是AC、BC的中点.(1)若AC=9cm,CB=7cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=20cm,其它条件不变,你能猜想MN的长度吗?并说明理由
(3)若已知线段AB=a,若C在线段AB的延长线上,且满足M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并写出你的结论.
分析 (1)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案;
(3)根据线段中点的性质,可得MC、CN,再根据线段的和差,可得答案.
解答 解:(1)由M、N分别是AC、BC的中点,
得MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由线段的和差,得MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$×9+$\frac{1}{2}$×7=8cm;
(2)MN=10cm,理由如下:
由M、N分别是AC、BC的中点,
得MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由线段的和差,得MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=10cm;
(3)MN=$\frac{a}{2}$,理由如下:
由M、N分别是AC、BC的中点,
得MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由线段的和差,得MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB=$\frac{a}{2}$;
如图: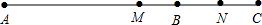 ,
,
只要满足点C在线段AB所在直线上,点M、N分别是AC、BC的中点.那么MN就等于AB的一半.
点评 本题考查了两点间的距离,利用了线段中点的性质,线段的和差.

练习册系列答案
相关题目
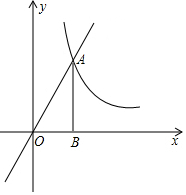 已知图中的曲线是反比例函数y=$\frac{m-5}{x}$(m为常数)图象的一支.
已知图中的曲线是反比例函数y=$\frac{m-5}{x}$(m为常数)图象的一支.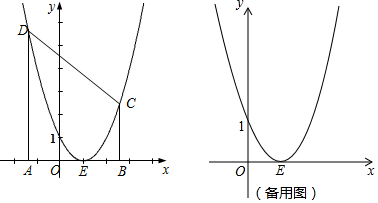
 如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.
 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为2.
如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为2.