题目内容
13.已知:直线AB与直线CD相交于点O,∠BOC=40°.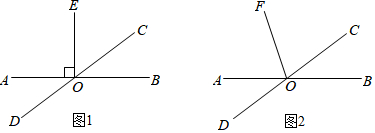
(1)如图1,若∠AOE=90°,求∠DOE的度数;
(2)如图2,若OF平分∠AOC,求∠DOF的度数.
分析 (1)根据对顶角的性质可得∠AOD=∠BOC,再根据∠AOE=90°,再利用角的和差关系可得答案;
(2)首先根据邻补角定义可得∠AOC的度数,再根据角平分线的性质可得∠AOF的度数,然后再利用角的和差关系求出∠DOF的度数.
解答  解:(1)∵直线AB与直线CD相交于O,
解:(1)∵直线AB与直线CD相交于O,
∴∠AOD=∠BOC=40°,
∵∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=130°;
(2)∵∠BOC=40°,
∴∠AOC=140°,∠AOD=40°,
∵FO平分∠AOC,
∴∠AOF=$\frac{1}{2}$∠AOC=70°,
∴∠DOF=∠AOD+∠AOF=110°.
点评 此题主要考查了角平分线,以及垂线和邻补角,关键是掌握对顶角的性质:对顶角相等;邻补角的性质:邻补角互补,即和为180°.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.方程x(x-1)=x的解是( )
| A. | x=0 | B. | x=2 | C. | x1=0,x2=1 | D. | x1=0,x2=2 |
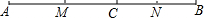 如图,点C在线段AB上,点M.N分别是AC、BC的中点.
如图,点C在线段AB上,点M.N分别是AC、BC的中点.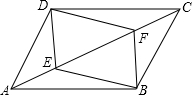 已知:如图,点E和点F是平行四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.求证:四边形DEBF为平行四边形.
已知:如图,点E和点F是平行四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.求证:四边形DEBF为平行四边形.



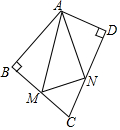 如图,在四边形ABCD中,∠BAD=110°,∠B=∠D=90°.在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的度数为140°.
如图,在四边形ABCD中,∠BAD=110°,∠B=∠D=90°.在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的度数为140°. 实数a在数轴上的位置如图所示,则$\sqrt{({a-3)}^{2}}$=3-a.
实数a在数轴上的位置如图所示,则$\sqrt{({a-3)}^{2}}$=3-a.