��Ŀ����
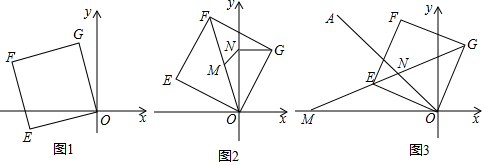
19����ͼ����֪�����ߵĶ�������ΪE��1��0������y��Ľ�������Ϊ��0��1������1����������ߵĺ�����ϵʽ��
��2��A��B��x�����������㣬��A��B��ľ���ΪAB=4��A��B����ߣ���A��AD��x�ύ��������D����B��BC��x�ύ��������C��
�ٵ�CD��x��ʱ���ı���ABCD�������Σ�
�ڵ�CD��x��ʱ�����߶�BD���Ƿ���������ĵ�P��ʹ�á�PAE���ܳ���С�������ڣ�ֱ��д����P�����꼰��ʱ��PAE���ܳ����������ڣ�˵�����ɣ�
��3���ڣ�2���Ļ����ϣ�ֱ��BD���Ƿ���������ĵ�Q��ʹ�á�BAQ���ACE���ƣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
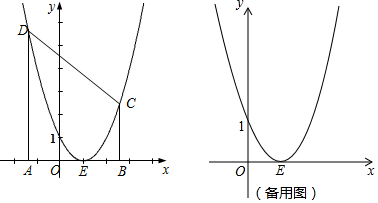
���� ��1���������ߵĽ���ʽΪ��y=a��x-1��2���ѵ㣨0��1�����������ߵĽ���ʽ���a��ֵ���ɣ�
��2����������������A��B��C��D�����꣬�Ӷ��ɶ��ı���ABCD����״�����жϣ�������CE��BD���P��������ԳƵ����ʿ�֪AP=PC���ʴ˵�E��P��C��һ��ֱ����ʱ����APE���ܳ���С��Ȼ�����ֱ��EC��ֱ��BD�Ľ���ʽ���ɺ�������ʽ�������ֱ�ߵĽ���P�����꣬Ȼ�����CE�ij�����������ݡ�PAE���ܳ�=AE+EC��⼴�ɣ�
��3������Q��QF��AB������ΪF����$\frac{QB}{AB}$=$\frac{AE}{AC}$ʱ����BAQ���ACE���ƣ��Ӷ������BQ�ij���Ȼ����Rt��QFB�����QF��BF�ij������ǿɵõ���Q�����꣮
��� �⣺��1���������ߵĽ���ʽΪ��y=a��x-1��2���ѵ㣨0��1�������������У�1=a��0-1��2���ã�a=1��
���������ߵĽ���ʽΪ��y=��x-1��2��
��2���١�AD��BC��AB=4��E��1��0����
��A��-1��0����B��3��0����
��x=-1ʱ��y=4����x=3ʱ��y=4��
��D��-1��4����C��3��4����
���ı���ABCD�������Σ�
�ʴ�Ϊ��������
����ͼ��ʾ��
���ı���ABCD�Ǿ��Σ�
���A��C����BD�Գƣ�ֱ��CE��BD�Ľ�����ǵ�P��
��ʱ��A��-1��0����B��3��0����C��3��4����D��-1��4����E��1��0����
��Rt��BEC�У����ݹ��ɶ��������EC=2$\sqrt{5}$��
��ֱ��CE�Ľ���ʽΪy=kx+b������E�͵�C����������$\left\{\begin{array}{l}{k+b=0}\\{3k+b=4}\end{array}\right.$����ã�k=2��b=-2��
��ֱ��CE�Ľ���ʽ��y=2x-2��
��ֱ��BD�Ľ���ʽ��y=mx+n������B��D���������ã�$\left\{\begin{array}{l}{3m+n=0}\\{-m+n=4}\end{array}\right.$����ã�m=-1��n=3��
��ֱ��BD�Ľ���ʽΪy=-x+3��
��y=2x-2��y=-x+3�����ã�$\left\{\begin{array}{l}{y=2x-2}\\{y=-x+3}\end{array}\right.$����ã�x=$\frac{5}{3}$��y=$\frac{4}{3}$��
���P��������$\frac{5}{3}$��$\frac{4}{3}$����
���PAE���ܳ�=AE+EC=2+2$\sqrt{5}$��
��3����ͼ��ʾ������Q��QF��AB������ΪF��
���ı���ABCDΪ�����Σ�
���QBA=��CAE=45�㣮
�൱$\frac{QB}{AB}$=$\frac{AE}{AC}$ʱ����BAQ���ACE���ƣ�
��$\frac{BQ}{4}$=$\frac{2}{4\sqrt{2}}$����ã�BQ=$\sqrt{2}$��
��Rt��QFB�У���QBF=45�㣬
��QF=BF=$\frac{\sqrt{2}}{2}$��$\sqrt{2}$=1��
���Q��������2��1����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ�����ɶ�������Գ�·��������⡢���������ε��ж������������������֪ʶ�ǽ���Ĺؼ���

| A�� | ab��abc | B�� | -mn��2mn | C�� | 0.5x3y2��2x2y3 | D�� | xy2��xz2 |




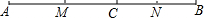 ��ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮
��ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮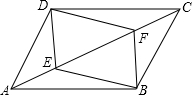 ��֪����ͼ����E�͵�F��ƽ���ı���ABCD�ĶԽ���AC�ϵ����㣬AF=CE������DE��DF��BE��BF����֤���ı���DEBFΪƽ���ı��Σ�
��֪����ͼ����E�͵�F��ƽ���ı���ABCD�ĶԽ���AC�ϵ����㣬AF=CE������DE��DF��BE��BF����֤���ı���DEBFΪƽ���ı��Σ�