题目内容
已知直线MN是线段BC的垂直平分线,垂足为O,点P为射线OM上的一点,连接BP、PC.将线段PB绕点P逆时针
旋转,得到线段PQ(PQ与PC不重合),旋转角为α(0°<α<180°)直线CQ交MN与点D连接ED.
(1)如图1,当α=30°,且点P与点O重合时,∠CDM的度数是 ;
(2)如图2,当α=120°,且点P与点O不重合时,∠CDM的度数是 ;
(3)点P在射线OM上运动时,∠CDM的度数是 .(用含α的代数式表示)

旋转,得到线段PQ(PQ与PC不重合),旋转角为α(0°<α<180°)直线CQ交MN与点D连接ED.
(1)如图1,当α=30°,且点P与点O重合时,∠CDM的度数是
(2)如图2,当α=120°,且点P与点O不重合时,∠CDM的度数是
(3)点P在射线OM上运动时,∠CDM的度数是

考点:旋转的性质
专题:
分析:(1)由中垂线的性质就可以得出BO=CO,由旋转的性质可以出PQ=OB=PC,由三角形外角与内角的关系就可以得出∠C=15°,在△PDC中可以求出∠CDM的结论;
(2)由轴对称的性质可以得出△PBD≌△PCD,就有∠PBD=∠PCD,∠PDB=∠PDC,就可以得出∠PQC+∠PQD=180°,得出∠PQD+∠PBD=180°,由四边形的内角和就可以得出∠BPQ+∠BDC=180°,进而就可以得出∠CDM的值.
(3)由轴对称的性质可以得出△PBD≌△PCD,就有∠PBD=∠PCD,∠PDB=∠PDC,就可以得出∠PQC+∠PQD=180°,得出∠PQD+∠PBD=180°,由四边形的内角和就可以得出∠BPQ+∠BDC=180°,进而就可以得出∠CDM=
(180°-a)=90°-
a.
(2)由轴对称的性质可以得出△PBD≌△PCD,就有∠PBD=∠PCD,∠PDB=∠PDC,就可以得出∠PQC+∠PQD=180°,得出∠PQD+∠PBD=180°,由四边形的内角和就可以得出∠BPQ+∠BDC=180°,进而就可以得出∠CDM的值.
(3)由轴对称的性质可以得出△PBD≌△PCD,就有∠PBD=∠PCD,∠PDB=∠PDC,就可以得出∠PQC+∠PQD=180°,得出∠PQD+∠PBD=180°,由四边形的内角和就可以得出∠BPQ+∠BDC=180°,进而就可以得出∠CDM=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵直线MN是线段BC的垂直平分线,
∴BO=CO,∠COD=90°.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠Q=∠C.
∵∠Q+∠C=∠BPQ=30°,
∴∠C=15°,
∴∠C+∠CDM=90°,
∴∠CDM=75°.
故答案为:75°
(2)如图2,∵直线MN是线段BC的垂直平分线,
∴PB=PC,BD=CD.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠PQC=PCQ.
在△PBD和△PCD中
,
∴△PBD≌△PCD(SSS),
∴∠PBD=∠PCD,∠PDB=∠PDC,
∴∠PBD=∠PCD=∠PQC.
∵∠PQC+∠PQD=180°,
∴∠PQD+∠PBD=180°.
∵∠PBD+∠BDQ+∠DQP+∠BPQ=360°,
∴∠BPQ+∠BDC=180°.
∵∠BPQ=120°,
∴∠BDC=60°.
∵∠PDB=∠PDC,
∴∠PDC=30°.
即∠CDM=30°.
故答案为:30°;
(3)∵直线MN是线段BC的垂直平分线,
∴PB=PC,BD=CD.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠PQC=PCQ.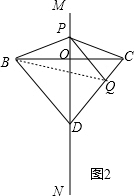
在△PBD和△PCD中
,
∴△PBD≌△PCD(SSS),
∴∠PBD=∠PCD,∠PDB=∠PDC,
∴∠PBD=∠PCD=∠PQC.
∵∠PQC+∠PQD=180°,
∴∠PQD+∠PBD=180°.
∵∠PBD+∠BDQ+∠DQP+∠BPQ=360°,
∴∠BPQ+∠BDC=180°.
∵∠BPQ=a,
∴∠BDC=180°-a.
∵∠PDB=∠PDC,
∴∠PDC=90°-
a.
即∠CDM=90°-
a.
故答案为:90°-
a.
∴BO=CO,∠COD=90°.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠Q=∠C.
∵∠Q+∠C=∠BPQ=30°,
∴∠C=15°,
∴∠C+∠CDM=90°,
∴∠CDM=75°.
故答案为:75°
(2)如图2,∵直线MN是线段BC的垂直平分线,
∴PB=PC,BD=CD.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠PQC=PCQ.
在△PBD和△PCD中
|
∴△PBD≌△PCD(SSS),
∴∠PBD=∠PCD,∠PDB=∠PDC,
∴∠PBD=∠PCD=∠PQC.
∵∠PQC+∠PQD=180°,
∴∠PQD+∠PBD=180°.
∵∠PBD+∠BDQ+∠DQP+∠BPQ=360°,
∴∠BPQ+∠BDC=180°.
∵∠BPQ=120°,
∴∠BDC=60°.
∵∠PDB=∠PDC,
∴∠PDC=30°.
即∠CDM=30°.
故答案为:30°;
(3)∵直线MN是线段BC的垂直平分线,
∴PB=PC,BD=CD.
∵段PB绕点P逆时针旋转,得到线段PQ
∴PB=PC=PQ.
∴∠PQC=PCQ.

在△PBD和△PCD中
|
∴△PBD≌△PCD(SSS),
∴∠PBD=∠PCD,∠PDB=∠PDC,
∴∠PBD=∠PCD=∠PQC.
∵∠PQC+∠PQD=180°,
∴∠PQD+∠PBD=180°.
∵∠PBD+∠BDQ+∠DQP+∠BPQ=360°,
∴∠BPQ+∠BDC=180°.
∵∠BPQ=a,
∴∠BDC=180°-a.
∵∠PDB=∠PDC,
∴∠PDC=90°-
| 1 |
| 2 |
即∠CDM=90°-
| 1 |
| 2 |
故答案为:90°-
| 1 |
| 2 |
点评:本题考查了旋转的性质运用,中垂线的性质的运用,全等三角形的判定与性质的运用,四边形内角和定理的运用,等腰三角形的性质的运用,解答时灵活运用旋转的性质求解是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、x2+4=0,则x=±2 |
| B、x2=x的根为x=1 |
| C、x2-2x=3没有实数根 |
| D、4x2+9=12x有两个相等的实数根 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则正确的结论是( )| A、abc>0 |
| B、3a+c<0 |
| C、4a+2b+c<0 |
| D、b2-4ac<0 |
若2:3=7:x,则x=( )
| A、2 | B、3 | C、3.5 | D、10.5 |
下列计算正确的是( )
| A、a2•a4=a8 |
| B、(-a2b3)2=a4b9 |
| C、a6÷a2=a3 |
| D、a2-2a2=-a2 |
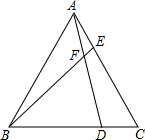 如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.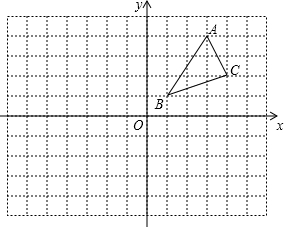 如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标.
如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标.