题目内容
17．在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点为整点，若整点P（m+2，$\frac{1}{2}$m-1）在第四象限，则m的值为0．分析 根据第四象限内的点横坐标大于零，纵坐标小于零，可得答案．
解答 解：点P（m+2，$\frac{1}{2}$m-1）是第四象限的整点，得m+2＞0且$\frac{1}{2}$m-1＜0，
解得-2＜m＜2，
m=-1，0，1；
故答案为0．
点评 本题考查了点的坐标，利用第四象限内的点横坐标大于零，纵坐标小于零得出m的值是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
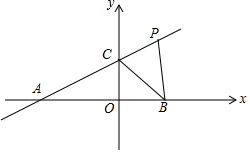若直线y=$\frac{1}{2}$x+2分别交x轴、y轴于A、C两点，点P是该直线上在第一象限内的一点，PB⊥x轴，B为垂足，且S△ABC=6
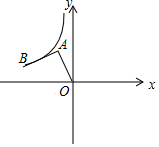如图，在平面直角坐标系中，点A（-1，2），将AO绕点A顺时针旋转90°，点O的对应点B恰好落在双曲线y=$\frac{k}{x}$的图象上，则k的值为-3．
如图是一大一小的两个可以自由转动的转盘，甲盘被平均分成6等份，乙盘被平均分成4等份，每个转盘均被涂上红、黄、蓝三种颜色，转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色，小明与小颖参与游戏；小明转动甲盘，小颖转动乙盘．