Question

15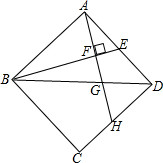．在正方形ABCD中，BE平分∠ABD，AH⊥BE于F，交BD于G，交CD于H，请写出所有与AE相等的线段，并证明．

Answer 1

分析 先由ASA证明△ABE≌△ADH（ASA），得出E=DH，再证明∠DGH=∠AHD，得出DH=DG，即可得出DG=DH=AE．

解答 解：DG=DH=AE；理由如下：
∵四边形ABCD是正方形，
∴AB=AD=CD，∠BAD=90°，∠ABD=∠ADB=45°，
∵BE平分∠ABD，AH⊥BE于F，
∴∠ABE=22.5°，∠AFB=90°，
∴∠BAF=90°-22.5°=67.5°，
∴∠DAH=22.5°，
∴∠ABE=∠DAH，
在△ABE和△ADH中，$\left\{\begin{array}{l}{∠ABE=∠DAH}&{\;}\\{AB=AD}&{\;}\\{∠BAE=∠ADH=90°}&{\;}\end{array}\right.$，
∴△ABE≌△ADH（ASA），
∴AE=DH，
∵∠AHD=90°-22.5°=67.5°，
∴∠DGH=180°-45°-67.5°=67.5°，
∴∠DGH=∠AHD，
∴DH=DG，
∴DG=DH=AE．

点评 本题考查了正方形的性质、全等三角形的判定与性质以及等腰三角形的判定方法；证明三角形全等和角相等是解决问题的关键．