题目内容
14.观察下列一组式的变形过程,然后回答问题:例1:$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-1}$=$\frac{\sqrt{2}-1}{1}$=$\sqrt{2}$-1.
例2:$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$,$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}$-$\sqrt{3}$,$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\sqrt{5}$-$\sqrt{4}$
利用以上结论解答以下问题:
(1)$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\sqrt{6}$-$\sqrt{5}$;$\frac{1}{\sqrt{100}+\sqrt{99}}$=$\sqrt{100}$-$\sqrt{99}$;
(2)你用含n(n为正整数)的关系式表示上述各式子的变形规律.$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$
(3)应用上面的结论,求下列式子的值.
$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$
(4)拓展提高,求下列式子的值.
$\frac{1}{1+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{5}}$+$\frac{1}{\sqrt{5}+\sqrt{7}}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2017}}$.
分析 (1)将$\frac{1}{\sqrt{6}+\sqrt{5}}$、$\frac{1}{\sqrt{100}+\sqrt{99}}$分母有理化,有理化因式分别为$\sqrt{6}-\sqrt{5}$、$\sqrt{100}-\sqrt{99}$;
(2)被开方数是两个相邻的数,即$\sqrt{n+1}+\sqrt{n}$,它的有理化因式为$\sqrt{n+1}-\sqrt{n}$,写出规律即可;
(3)由(1)(2)得,原式=$\sqrt{2}-1$+$\sqrt{3}-\sqrt{2}$+$\sqrt{4}-\sqrt{3}$+…+$\sqrt{100}-\sqrt{99}$,合并可得结果;
(4)先将分母根据加法交换律变形,再依次分母有理化,注意分母为2,提取$\frac{1}{2}$后可得结果.
解答 解:(1)$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\sqrt{6}-\sqrt{5}$,
$\frac{1}{\sqrt{100}+\sqrt{99}}$=$\sqrt{100}-\sqrt{99}$,
故答案为:$\sqrt{6}-\sqrt{5}$;$\sqrt{100}-\sqrt{99}$;
(2)由题意得变形规律为:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$,
故答案为:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$;
(3)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$,
=$\sqrt{2}-1$+$\sqrt{3}-\sqrt{2}$+$\sqrt{4}-\sqrt{3}$+…+$\sqrt{100}-\sqrt{99}$,
=-1+$\sqrt{100}$,
=-1+10,
=9;
(4)$\frac{1}{1+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{5}}$+$\frac{1}{\sqrt{5}+\sqrt{7}}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2017}}$,
=$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2015}}$,
=$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{5}-\sqrt{3}}{2}$+$\frac{\sqrt{7}-\sqrt{5}}{2}$+…+$\frac{\sqrt{2017}-\sqrt{2015}}{2}$,
=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{2017}$-$\sqrt{2015}$),
=$\frac{1}{2}$(-1+$\sqrt{2017}$),
=$\frac{\sqrt{2017}-1}{2}$.
点评 本题考查了分母有理化和平方差公式的运用,找规律是解决此题的关键,注意有理化因式的确定.


| A. | 三个 | B. | 四个 | C. | 五个 | D. | 六个 |
| A. | ±$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 4 | D. | ±4 |
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,∠AON=∠AOD+15°,求∠DON的度数.
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,∠AON=∠AOD+15°,求∠DON的度数.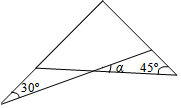 一副三角板如图所示叠放在一起,则∠α的度数是15°.
一副三角板如图所示叠放在一起,则∠α的度数是15°. 如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B.