题目内容
14. 科技馆是少年儿童节假日游玩的乐园.
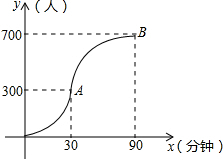
科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y=$\left\{\begin{array}{l}{a{x}^{2},0≤x≤30}\\{b(x-90)^{2}+n,30≤x≤90}\end{array}\right.$,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
分析 (1)构建待定系数法即可解决问题.
(2)先求出馆内人数等于684人时的时间,再求出直到馆内人数减少到624人时的时间,即可解决问题.
解答 解(1)由图象可知,300=a×302,解得a=$\frac{1}{3}$,
n=700,b×(30-90)2+700=300,解得b=-$\frac{1}{9}$,
∴y=$\left\{\begin{array}{l}{\frac{1}{3}{x}^{2}}&{(0≤x≤30)}\\{-\frac{1}{9}(x-90)^{2}+700}&{(30≤x≤90)}\end{array}\right.$,
(2)由题意-$\frac{1}{9}$(x-90)2+700=684,
解得x=78,
∴$\frac{684-624}{4}$=15,
∴15+30+(90-78)=57分钟
所以,馆外游客最少等待57分钟.
点评 本题考查二次函数的应用、一元二次方程等知识,解题的关键是熟练掌握待定系数法,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.将根号外的式子移到根号内:m$\sqrt{-\frac{1}{m}}$=( )
| A. | $\sqrt{-m}$ | B. | -$\sqrt{m}$ | C. | -$\sqrt{-m}$ | D. | 1 |
5.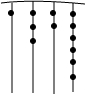 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )| A. | 84 | B. | 336 | C. | 510 | D. | 1326 |
3.下列图案既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.若关于x的不等式组$\left\{\begin{array}{l}{x>a}\\{x<2}\end{array}\right.$恰有3个整数解,则字母a的取值范围是( )
| A. | a≤-1 | B. | -2≤a<-1 | C. | a<-1 | D. | -2<a≤-1 |
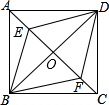 如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)