题目内容
19.已知a+b=8,a2b2=4,则$\frac{{a}^{2}+{b}^{2}}{2}$-ab=28或36.分析 根据条件求出ab,然后化简$\frac{{a}^{2}+{b}^{2}}{2}$-ab=$\frac{(a+b)^{2}}{2}$-2ab,最后代值即可.
解答 解:$\frac{{a}^{2}+{b}^{2}}{2}$-ab=$\frac{(a+b)^{2}-2ab}{2}$-ab=$\frac{(a+b)^{2}}{2}$-ab-ab=$\frac{(a+b)^{2}}{2}$-2ab
∵a2b2=4,
∴ab=±2,
①当a+b=8,ab=2时,$\frac{{a}^{2}+{b}^{2}}{2}$-ab=$\frac{(a+b)^{2}}{2}$-2ab=$\frac{64}{2}$-2×2=28,
②当a+b=8,ab=-2时,$\frac{{a}^{2}+{b}^{2}}{2}$-ab=$\frac{(a+b)^{2}}{2}$-2ab=$\frac{64}{2}$-2×(-2)=36,
故答案为28或36.
点评 此题是完全平方公式,主要考查了完全平方公式的计算,平方根的意义,解本题的关键是化简原式,难点是求出ab.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
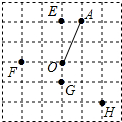

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
11.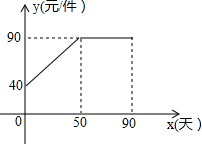 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元). | 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
9.小明和爸爸一起做投篮游戏,两人商定:小明投中1个得3分,爸爸投中1个得1分,结果两人一共投中20个,两人的得分恰好相等,设小明投中x个,爸爸投中y个,根据题意,列方程组为( )
| A. | $\left\{\begin{array}{l}{3x+y=20}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=20}\\{x=y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=20}\\{3x=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=20}\\{x=3y}\end{array}\right.$ |
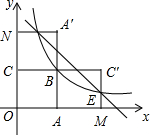 如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).
如图,四边形OABC是边长为2的正方形,函数y=$\frac{k}{x}(x>0)$的图象经过点B,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′,NA′BC.设线段MC′,NA′分别与函数y=$\frac{k}{x}(x>0)$的图象交于点E、F,则直线EF与x轴的交点坐标为(5,0).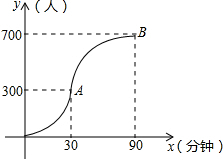 科技馆是少年儿童节假日游玩的乐园.
科技馆是少年儿童节假日游玩的乐园.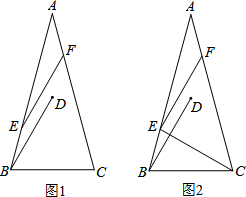 在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.