题目内容
6.如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.(1)求证:AB∥CD;
(2)若平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律,若不变,求出这两个角的比值;
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

分析 (1)根据平行线的性质,以及等量代换证明∠A+∠ABC=180°,即可证得AB∥CD;
(2)根据三角形外角的性质可直接得出结论;
(3)根据平行线的性质得到∠ABC=80°,设∠CBD=∠FBD=∠FDB=x°,根据角平分线的性质得到∠EBD=40°,于是得到∠AEB=x°+40°.得到∠BDC=80°-x°,根据∠AFC=∠ADB,列方程即可得到结论.
解答 (1)证明:∵AM∥BN,
∴∠A+∠ABC=180°,
又∵∠BCD=∠A,
∴∠ABC+∠BCD=180°,
∴AB∥CD;
(2)∵AM∥BN,∴∠ADB=∠DBC,∵BD平分∠FBC,∴∠FBD=∠DBC,
∴∠FBD=∠FDB,
当CD向右平移时,∠FBD增大,∠ABC不变,
∵∠FBD=∠FDB,∠BFA=∠FBD+∠FDB,∴∠AFB:∠ADB=2:1;
(3)存在,
理由:∵∠A=100°,∴∠ABC=80°,
设∠CBD=∠FBD=∠FDB=x°,
∵BE平分∠ABF,BD平分∠FBC,
∴∠EBD=40°
∴∠AEB=x°+40°.
∵AM∥BN,∠BCD=100°,
∴∠CDA=80°,
∴∠BDC=80°-x°,
∵∠AFC=∠ADB,
∴x°+40°=80°-x°,解得x=20°,
∴∠ADB=80°-20°=60°.
点评 此题考查了平行线的性质与平行四边形的性质.此题难度适中,解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
16.某工程队计划在10天内修路8km,前两天一共修完了2km,由于计划发生变化,准备提前两天完成修路任务,以后几天内平均每天至少要修路( )
| A. | 1km | B. | 0.9km | C. | 0.8km | D. | 0.6km |
11.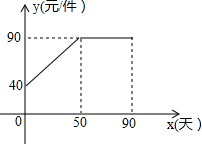 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元). | 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
18.下列能用平方差公式计算得是( )
| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(y+2) | D. | (2x+y)(2y-x) |
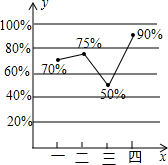 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题: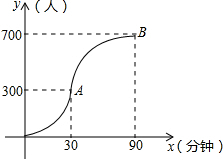 科技馆是少年儿童节假日游玩的乐园.
科技馆是少年儿童节假日游玩的乐园.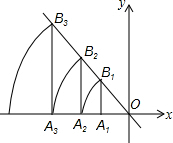 如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).
如图,直线l:y=-$\frac{4}{3}$x,点A1坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为(-$\frac{{5}^{2015}}{{3}^{2014}}$,0).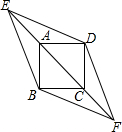 已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是16+16$\sqrt{2}$.
已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是16+16$\sqrt{2}$.