题目内容
2.解方程组:$\left\{\begin{array}{l}{\frac{x+y}{3}=\frac{z+x}{5}=\frac{y+z}{7}}\\{x+y+z=45}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{2x+5y-3z=0①}\\{7x-5y+2z=0②}\\{x+y+z=45③}\end{array}\right.$,
①+②得:9x-z=0④,
②+③×5得:12x+7z=225⑤,
④×7+⑤得:75x=225,即x=3,
把x=3代入④得:z=27,
把x=3,z=27代入③得:y=15,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=15}\\{z=27}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
13. 如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )
如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )
 如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )
如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
7.下列式子:3a2+1,-5,-a,-2x2y,-$\frac{3}{x^2}$,其中单项式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
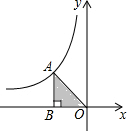 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过点A向x轴做垂线,垂足为B,若△ABO的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过点A向x轴做垂线,垂足为B,若△ABO的面积为6,则k的值为( )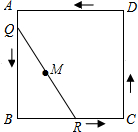 如图,有一条长度为1的线段QR,其端点Q、R在边长为1的正方形ABCD的四边上滑动一周时,QR的中点M所经过的路线长为π.
如图,有一条长度为1的线段QR,其端点Q、R在边长为1的正方形ABCD的四边上滑动一周时,QR的中点M所经过的路线长为π.