题目内容
17.先化简,再求值:$\frac{a+b}{ab}$÷(2-$\frac{a}{b}$-$\frac{b}{a}$),其中a、b的值是方程组$\left\{\begin{array}{l}{2(a+b)-(a-b)=3}\\{(a+b)-2(a-b)=1}\end{array}\right.$的解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出方程组的解得到a与b的值,代入计算即可求出值.
解答 解:原式=$\frac{a+b}{ab}$÷$\frac{2ab-{a}^{2}-{b}^{2}}{ab}$=$\frac{a+b}{ab}$•$\frac{ab}{(a-b)^{2}}$=-$\frac{a+b}{(a-b)^{2}}$,
方程组整理得:$\left\{\begin{array}{l}{a+b=\frac{5}{3}}\\{a-b=\frac{1}{3}}\end{array}\right.$,
则原式=-15.
点评 此题考查了分式方程化简求值,以及二元一次方程组的解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
8.下列多项式,不能运用平方差公式分解的是( )
| A. | -m2+4 | B. | -x2-y2 | C. | x2y2-1 | D. | (m+n)2-(a+b)2 |
5.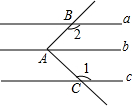 如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )
如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )
 如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )
如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )| A. | 180° | B. | 210° | C. | 270° | D. | 360° |
3.地球上陆地的面积约为149000000km2,数149000000用科学记数法可表示为( )
| A. | 1.49×108 | B. | 1.49×109 | C. | 14.9×108 | D. | 14.9×109 |