Question

6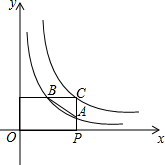．如图，已知反比例函数y=$\frac{a}{x}$和y=$\frac{b}{x}$（a≠0，b≠0），P（c，0）是x轴上的一个动点，过点P作x轴的垂线分别交y=$\frac{a}{x}$和y=$\frac{b}{x}$的图象于点A，C，过点C作y轴的垂线交y=$\frac{a}{x}$的图象于点B，连接AB，设△ABC的面积为S．
（1）当a=1，b=4，c=3时，求S的值；
（2）若a=1，b=4，c＞0，根据这些条件能否求出S的值？请说明理由．

Answer 1

分析 （1）根据已知条件求得y=$\frac{1}{x}$，y=$\frac{4}{x}$，P（3，0），于是得到A（3，$\frac{1}{3}$），C（3，$\frac{4}{3}$），B（$\frac{3}{4}$，$\frac{4}{3}$），根据三角形的面积公式即可得到结论；
（2）根据已知条件得到y=$\frac{1}{x}$，y=$\frac{4}{x}$，P（c，0），于是得到A（c，$\frac{1}{c}$），C（c，$\frac{4}{c}$），B（$\frac{c}{4}$，$\frac{4}{c}$），根据三角形的面积公式即可得到结论．

解答 解：∵a=1，b=4，c=3，
∴y=$\frac{1}{x}$，y=$\frac{4}{x}$，P（3，0），
∴A（3，$\frac{1}{3}$），C（3，$\frac{4}{3}$），B（$\frac{3}{4}$，$\frac{4}{3}$），
∴S=$\frac{1}{2}$AC•BC=$\frac{1}{2}×$1×$\frac{9}{4}$=$\frac{9}{8}$；

（2）根据这些条件能求出S的值，
∵a=1，b=4，c＞0，
∴y=$\frac{1}{x}$，y=$\frac{4}{x}$，P（c，0），
∴A（c，$\frac{1}{c}$），C（c，$\frac{4}{c}$），B（$\frac{c}{4}$，$\frac{4}{c}$），
∴S=$\frac{1}{2}$AC•BC=$\frac{1}{2}×$（$\frac{4}{c}$-$\frac{1}{c}$）×（c-$\frac{c}{4}$）=$\frac{9}{8}$，
∴根据这些条件能求出S的值．

点评 本题考查了反比例函数系数k的几何意义，三角形的面积，熟练掌握反比例函数系数k的几何意义是解题的关键．