题目内容
7. 看图填空,并在括号内说明理由:
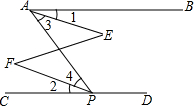
看图填空,并在括号内说明理由:如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
∵∠BAP与∠APD互补,已知
∴AB∥CD,同旁内角互补,两直线平行
∴∠BAP=∠APC.两直线平行,内错角相等
又∵∠1=∠2,已知
∴∠BAP-∠1=∠APC-∠2,等量代换
即∠3=∠4,∴AE∥PF,内错角相等,两直线平行
∴∠E=∠F.两直线平行,内错角相等.
分析 先根据题意得出AB∥CD,再由平行线的性质得出∠BAP=∠APC,根据∠1=∠2可得出∠3=∠4,进而得出AE∥PF,据此可得出结论.
解答 证明:∵∠BAP与∠APD互补(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠BAP=∠APC( 两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠BAP-∠1=∠APC-∠2(等量代换),即∠3=∠4,
∴AE∥PF,(内错角相等,两直线平行),
∴∠E=∠F( 两直线平行,内错角相等).
故答案为:已知;同旁内角互补,两直线平行;两直线平行,内错角相等;已知;等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定与性质定理是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.下列图形中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
15.计算x4•x3÷x2等于( )
| A. | x3 | B. | x4 | C. | x5 | D. | x6 |
12.当5个整数从小到大排列,其中位数是4,如果这组数据的唯一众数是6,则5个整数的和最大是( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
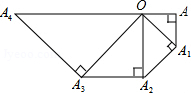 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA5的长度为4$\sqrt{2}$.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA5的长度为4$\sqrt{2}$.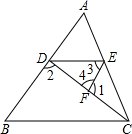 如图,∠1+∠2=180°,你能判断∠ADE与∠3之间的大小关系吗?请说明理由.
如图,∠1+∠2=180°,你能判断∠ADE与∠3之间的大小关系吗?请说明理由. 如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.
如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是210cm.