题目内容
16.定义新运算:若$\stackrel{→}{m}$=(a,b),$\stackrel{→}{n}$=(c,d),则$\stackrel{→}{m}$•$\stackrel{→}{n}$=ac-bd;若$\stackrel{→}{m}$=(1,2),$\stackrel{→}{n}$=(3,5),则$\stackrel{→}{m}$•$\stackrel{→}{n}$=1×3-2×5=-7;
(1)已知$\stackrel{→}{m}$=(2,4),$\stackrel{→}{n}$=(2,-3),求$\stackrel{→}{m}$•$\stackrel{→}{n}$;
(2)已知$\stackrel{→}{m}$=(x-a,1),$\stackrel{→}{n}$=(2x,x+1),令y=$\stackrel{→}{m}$•$\stackrel{→}{n}$,求y,并思考y=$\stackrel{→}{m}$•$\stackrel{→}{n}$的函数图象与一次函数y=x+1的图象是否相交,请说明理由.
分析 (1)根据$\stackrel{→}{m}$•$\stackrel{→}{n}$=ac-bd,代入数据即可求出结论;
(2)根据$\stackrel{→}{m}$=(x-a,1)、$\stackrel{→}{n}$=(2x,x+1)结合$\stackrel{→}{m}$•$\stackrel{→}{n}$=ac-bd即可找出y关于x的函数关系式,将其代入y=x+1中整理得x2-(a+1)x-1=0,再根据根的判别式△=b2-4ac=(a+1)2+4>0,即可得出y=$\stackrel{→}{m}$•$\stackrel{→}{n}$的函数图象与一次函数y=x+1的图象相交.
解答 解:(1)∵$\overrightarrow{m}$=(2,4),$\overrightarrow{n}$=(2,-3),
∴$\overrightarrow{m}$•$\overrightarrow{n}$=2×2-4×(-3)=16.
(2)两函数图象相交.理由如下:
∵$\stackrel{→}{m}$=(x-a,1),$\stackrel{→}{n}$=(2x,x+1),
∴y=$\stackrel{→}{m}$•$\stackrel{→}{n}$=(x-a)•2x-(x+1)=2x2-2ax-x-1=2x2-(2a+1)x-1.
将y=2x2-(2a+1)x-1代入y=x+1,整理得:x2-(a+1)x-1=0.
∵△=b2-4ac=(a+1)2+4>0,
∴方程有两个不相等的实数根,
∴两函数图象相交.
点评 本题考查了根的判别式以及直线与抛物线的交点问题,解题的关键是:(1)根据定义式$\stackrel{→}{m}$•$\stackrel{→}{n}$=ac-bd代入数据求值;(2)利用根的判别式△=b2-4ac=(a+1)2+4>0,找出y=$\stackrel{→}{m}$•$\stackrel{→}{n}$的函数图象与一次函数y=x+1的图象相交.

 阅读快车系列答案
阅读快车系列答案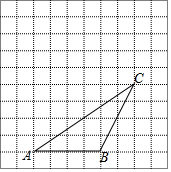 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移2格.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移2格.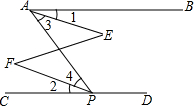 看图填空,并在括号内说明理由:
看图填空,并在括号内说明理由: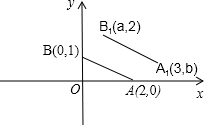 如图,A,B两点的坐标分别为(2,0)(0,1),若将线段AB平移至A1B1,则a+b的值为( )
如图,A,B两点的坐标分别为(2,0)(0,1),若将线段AB平移至A1B1,则a+b的值为( )
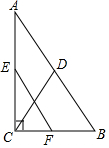 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,若EF=4,则CD的长为4.
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,若EF=4,则CD的长为4.